基本介紹
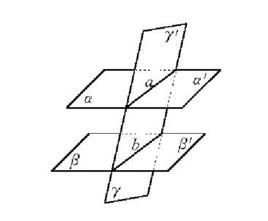
平行平面定理立體幾何的重要定理之一,如果一個平面與兩個平行平面同時相交,則在形成的三面八角幾何圖形中:
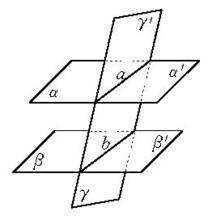 圖1
圖1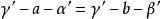 平行平面定理
平行平面定理1.同位二面角相等,如圖中的;
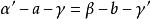 平行平面定理
平行平面定理2.內錯二面角相等,如圖中的;
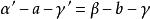 平行平面定理
平行平面定理3.外錯二面角相等,如圖中的;
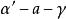 平行平面定理
平行平面定理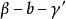 平行平面定理
平行平面定理4.同旁內二面角互補,如圖中的和互補;
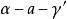 平行平面定理
平行平面定理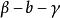 平行平面定理
平行平面定理5.同旁外二面角互補,如圖中的和互補 。
定理的證明
一平面和兩個平行平面相交,求證它們的同位二面角相等、內錯二面角也相等,同旁二面角互補。
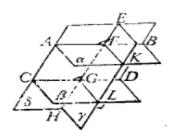 圖2
圖2分析:通過作與此三平面垂直的平面,得到平面上的三線八角,轉化為平面幾何問題證。
 平行平面定理
平行平面定理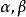 平行平面定理
平行平面定理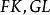 平行平面定理
平行平面定理 平行平面定理
平行平面定理 平行平面定理
平行平面定理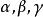 平行平面定理
平行平面定理證明:如圖2,設平面和兩平行平面相交,交線為,過交線FK上任意一點F作平面使與FK垂直,設平面與平面的交線分別為AB、CD、EH。
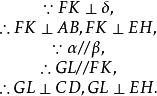 平行平面定理
平行平面定理 平行平面定理
平行平面定理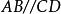 平行平面定理
平行平面定理則在平面內,,AB,CD與EH所成的角均為有關二面角的平面角。
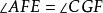 平行平面定理
平行平面定理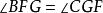 平行平面定理
平行平面定理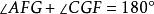 平行平面定理
平行平面定理由平面幾何可知,(同位角相等),(內!錯角相等),(同旁內角互補)。
而 具有相等平面角的兩個二面角相等,具有互補平面角的兩個二面角互補。
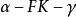 平行平面定理
平行平面定理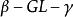 平行平面定理
平行平面定理所以: 二面角與二面角相等;
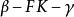 平行平面定理
平行平面定理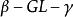 平行平面定理
平行平面定理二面角與二面角相等;
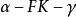 平行平面定理
平行平面定理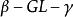 平行平面定理
平行平面定理二面角與二面角互補。
即同位二面角相等,內錯二面角相等,同旁二面角互補 。
平行平面的其他定理
定理1 如果一個平面平行於兩條相交直線,那么這個平面也就平行於這兩條相交直線所確定的平面。由這個定理,可以知道:如果一個平面內的兩條直線分別平行於另一個平面內的兩條相交直線,那么這兩個平面平行。
定理2垂直於同一條直線的兩個平面平行。
定理3 如果兩個平面都平行於第三個平面,那么這兩個平面也互相平行。
定理4 如果兩個平行平面之一與第三個平面相交,則另一個也與第三個平面相交。
定理5 如果兩個平行平面都和第三個平面相交,那么,它們的交線平行。
定理6如果一條直線垂直於兩個平行平面中的一個平面,那么這條直線也垂直於另一個平面 。