平行平面截直線定理

平行平面截直線定理，是指兩條直線穿過一組平行平面，則其各平面的交點所組成的線段成比例的一個立體幾何定理。

基本信息

• 中文名：平行平面截直線定理
• 英文名：theorem of cutting the line by parallel planes

• 適用範圍：數理科學
• 判定：都垂直於同一條直線
• 性質：和第三個平面的交線平行

簡介

平行平面截直線定理是立體幾何的重要定理之一。

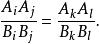平行平面截直線定理

如果α，α，...，α是一組平行平面，直線a，b都與它們相交，其交點分別為A，A，...，A與B，B，...，B（如圖），則對任何i,j,k,l∈{1,2,...,n},i≠j,k≠l，有

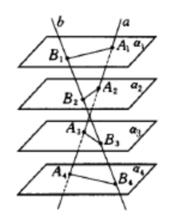圖1

兩平行平面的判定

下列條件每一個都可判定兩平面平行：

1、一個平面內有兩條相交直線都平行於另一個平面。

2、都垂直於同一條直線。

3、都平行於第三個平面。

4、一個平面內的兩條相交直線分別與另一個平面內的兩條相交直線平行。

兩平行平面的性質

兩平行平面的主要性質有：

1、它們和第三個平面的交線平行。

2、垂直於一個平面的直線也垂直於另一個平面。

3、和其中一個平面相交的直線必和另一個平面相交。

4、第三個平面和其中一個平面相交（或平行），必和另一平面也相交（或平行）。

5、其中一個平面上的任何一條直線都平行於另一個平面。

6、夾在它們間且與它們相交的平行線段相等；公垂線段的長相等。