兩平面平行的定義
兩平面平行是兩平面間的一種位置關係,如果兩個平面沒有公共點,我們說這兩個平面互相平行,一個平面稱為另一個平面的平行平面。
兩平面平行的性質定理
定理1 兩平面平行,其中一個平面內的直線必平行於另一個平面。
定理2 如果兩個平行平面同時和第三個平面相交,那么它們的交線平行。
定理3 一條直線垂直於兩個平行平面中的一個平面,它也垂直於另一個平面 。
例 如圖1,在正方體ABCD-ABCD中,M,N,P分別是CC,BC,CD的中點,求證:
(1)AP⊥MN;
(2)平面MNP∥平面ABD。
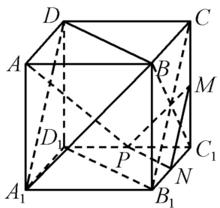 圖1
圖1證明 (1)連結BC,BC,則BC⊥BC,BC是AP在面BBCC上的射影,
∴ AP⊥BC.
又BC∥MN,
∴ AP⊥MN.
(2)連結BD.
∵ P,N分別是DC,BC的中點,
∴ PN∥BD.又BD∥BD,
∴ PN∥BD.
又PN不在平面ABD上,
∴ PN∥平面ABD.
同理,MN∥平面ABD.
又PN∩MN=N,
∴ 平面PMN∥平面ABD。
說明 將空間問題轉化為平面問題,是解決立體幾何問題的重要策略.解決這類問題關鍵在於選擇或添加適當的平面或線。由於M,N,P都為中點,故添加BC,BC作為聯繫的橋樑 。
兩平面平行的判定
 兩平面平行
兩平面平行設兩平面的方程分別為
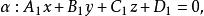 兩平面平行
兩平面平行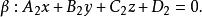 兩平面平行
兩平面平行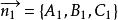 兩平面平行
兩平面平行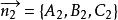 兩平面平行
兩平面平行其法線向量分別為和。
兩平面平行的充要條件:
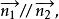 兩平面平行
兩平面平行即
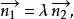 兩平面平行
兩平面平行用分量來表示為:
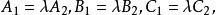 兩平面平行
兩平面平行亦即
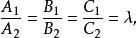 兩平面平行
兩平面平行或
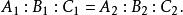 兩平面平行
兩平面平行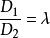 兩平面平行
兩平面平行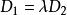 兩平面平行
兩平面平行 兩平面平行
兩平面平行若,即,則平面的方程為:
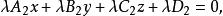 兩平面平行
兩平面平行即:
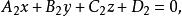 兩平面平行
兩平面平行與平面β的方程一致,所以兩平面重合,由此我們看出:
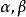 兩平面平行
兩平面平行兩平面平行的充要條件是
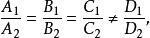 兩平面平行
兩平面平行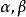 兩平面平行
兩平面平行兩平面重合的充要條件是
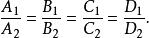 兩平面平行
兩平面平行兩平面相交
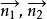 兩平面平行
兩平面平行即不平行,即
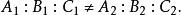 兩平面平行
兩平面平行這時兩平面相交時所得直線的方程可用方程組
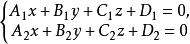 兩平面平行
兩平面平行來表示 。
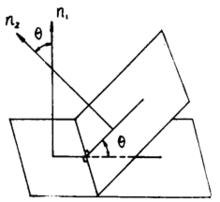 圖2
圖2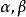 兩平面平行
兩平面平行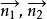 兩平面平行
兩平面平行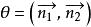 兩平面平行
兩平面平行為了確定起見,規定兩平面組成的二面角中,不大於直角的為兩平面的交角,記作θ,如圖2,所成的夾角θ就是兩法線向量的夾角θ,即(圖1),且
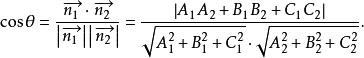 兩平面平行
兩平面平行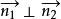 兩平面平行
兩平面平行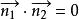 兩平面平行
兩平面平行特別地,當時,, 故又可以得兩平面互相垂直的充要條件為
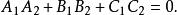 兩平面平行
兩平面平行