定義
帕施公理是順序公理組第四個公理。順序公理是基本的幾何公理之一，指希爾伯特-歐幾里得幾何系統公理表中的第二組公理，是建立點的位置關係的公理，包括以下四條：1.如果B點介於A和C兩點之間，那么A，B，C是一直線上的三個不同的點，並且B也介於C和A之間；2.對於任何不同的A，B兩點，在直線AB上至少有一點C，使得B介於A和C之間；3.在一直線上任何不同的三點中，至多有一點介於其餘兩點之間；4.( 帕施公理)設A，B，C是不在同一直線上的三點，a是平面ABC上的一直線，它不通過A，B，C中任何一點，如果a有一點介於A和B之間，那么a必還有一點介於A和C或B和C之間 。
帕施公理順序公理的1-3稱為線形的順序公理，因為這些是與在一直線上的點有關的緣故，與這些聯合的還有第四個，平面的順序公理，通稱“帕施公理”或“帕須公理”等，這是按最初明白地把它公式化的幾何學家的名字的，是德國數學家巴斯(M.Path，1843-1930)提出，是證明線段存在內點的主要工具 。
帕施公理與西爾維斯特問題
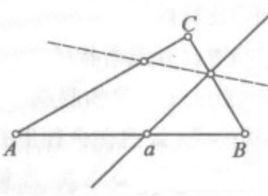
變分方法的一個特徵是，它經常導出非常簡短的證明，這方面的一個驚人例子是西爾維斯特(J.J.Sylvester)於1893年提出的著名問題：設S是平面上的一個有限點集，且任何經過其中兩個點的直線都一定經過其中另一個點，證明這些點都在一條直線上，不論是西爾維斯特還是他的同時代人都沒能找到一個證明，過了將近50年，才由加萊(Gallai)發表了第一個證明，但相當複雜。下面這個簡短的證明現已廣為人知，它是由凱利(L.M.Kelly)於1948年發現的(見《美國數學月刊》(Amer.Math.Monthly)55，P.28)。假設這些具有西爾維斯特所述性質的點不共線，每條經過其中兩點的直線L和不在這條直線上的一個點p都組成一個線點對(L，p)，在所有這些線點對中選取一個使得從p到L的距離d為最小的。令q為從p向L所引垂線的垂足。於是(變分)根據假設，在L上至少存在三個點a，b和c。因此其中兩個點，比方說a和b，將以a，b，q的順序位於q的同一側(c可在任何一側)，如圖1，但這樣從b到直線ap的距離d'就小於d，這就產生了一個矛盾 。
圖1 凱利的證明凱利的證明確實簡短——但是，這裡有考克斯特(H.S.M.Coxeter)的說法(見《幾何學導引》(Introduction to Geometry),Wiley,1961,p.181)：“這件關於共線性的事[西爾維斯特的問題]顯然屬於序幾何。[確實，在複數域或有限域上這個結果不成立！你可以輕易地在環面上發現一個九點的反例。]凱利的歐氏幾何式證明涉及外在的距離概念：這好比用一把長柄錘子去砸一個杏仁。真正恰當的堅果鉗由下述證明所提供。”
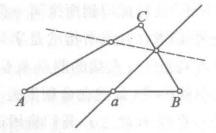
考克斯特的可愛的證明(很高興這個證明用的也是變分方法)依賴於帕施(Pasch)公理。這條公理以它最簡單的形式斷言：一條直線不可能只與一個二角形的一條邊相遇。(理解這條公理的一個方法是，把它看作若爾當(Jordan)曲線定理的一個非常初等的特例。如果這條直線通過一條邊進入這個三角形，那么它必定要穿過另一條邊以回到外面來。)這個證明的圖與凱利證明的圖非常相似，不過這次我們選取的是任意的點p，並找出一條從它出發的射線R，R上沒有S中其他點，但至少與一條連線S中點的直線相交，每條這樣的直線都與R相交於某點，於是我們可從中選取一條直線L，它與R的交點q距p最近(當然，不是在距離的意義下，而是把它們看作R上的一個序集。也就是說，在p和q之間沒有其他交點)，現在(變分)L上一定有兩個點a和b，它們位於q的同一側，我們證明直線ap上不可能有S中的另一個點，有兩種情況 。
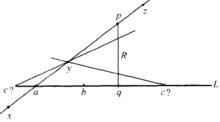圖2 運用帕施公理的證明情況1 另一個點y位於a和p之間。於是(如圖2)不論c在哪裡，將帕施公理套用於三角形apq，直線cy將與R相交於一個比q更近於p的點。
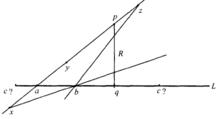圖3 運用帕施公理對另一種情況的證明情況2 另一個點x或z不在a和p之間，於是，同前面一樣，不是bx就是bz，將與R相交於一個比q更近於p的點，(見圖3) 。
