已知圓O的直徑為a，圓周上一點P，取P為極點，過P的一條直徑為極軸。考慮割線PQ與圓交於另一點Q，延長PQ到R，使QR=b，則Q的軌跡為帕斯卡蝸線。
直角坐標方程：(x^2+y^2-2ax)^2=b^2(x^2+y^2)
參數方程：x=acos(t)^2+bcos(t)
y=acos(t)sin(t)+bsin(t)
極坐標方程：ρ=2a*cosθ+b 。
曲線形狀
根據a、b的大小帕斯卡蝸線可以分為五種情況。
①b<a 曲線有一個大圈和一個小圈。
②b=a 曲線有一個尖點（原點）。此時為心臟線。
③a<b<2a 曲線的尖點開始離開原點，且逐漸由凹變平。
④b=2a 曲線的左端完全變平。
⑤b>2a 曲線的左端由平變凸。
帕斯卡蝸線就是外旋輪線的特殊情況
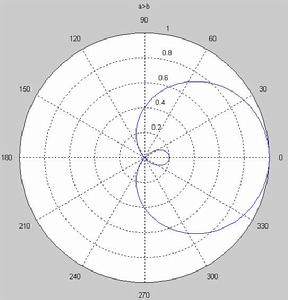帕斯卡蝸線 ab時