布洛赫定理

布洛赫波由一個平面波和一個周期函式u（r）（布洛赫波包）相乘得到。 可以看出，具有上式性質的波函式可以寫成布洛赫函式的形式。 ）的作用次序滿足交換律，所以周期勢場中粒子的本徵波函式總是可以寫成布洛赫函式的形式。

布洛赫波因其提出者美籍瑞士裔物理學家菲利克斯·布洛赫（Felix Bloch）而得名。
布洛赫波由一個平面波和一個周期函式u（r）（布洛赫波包）相乘得到。其中u（r）與勢場具有相同周期性。布洛赫波的具體形式為：

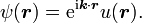
式中k 為波矢。上式表達的波函式稱為布洛赫函式。當勢場具有晶格周期性時，其中的粒子所滿足的波動方程的解ψ存在性質：

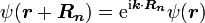
這一結論稱為布洛赫定理（Bloch's theorem），其中

為晶格周期矢量。可以看出，具有上式性質的波函式可以寫成布洛赫函式的形式。

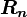
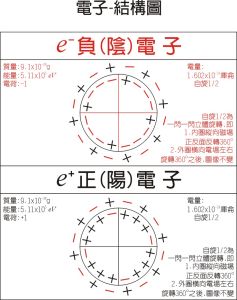電子-模型圖

平面波波矢k（又稱“布洛赫波矢”，它與約化普朗克常數的乘積即為粒子的晶體動量）表征不同原胞間電子波函式的位相變化，其大小只在一個倒易點陣矢量之內才與波函式滿足一一對應關係，所以通常只考慮第一布里淵區內的波矢。對一個給定的波矢和勢場分布，電子運動的薛丁格方程具有一系列解，稱為電子的能帶，常用波函式的下標n 以區別。這些能帶的能量在k的各個單值區分界處存在有限大小的空隙，稱為能隙。在第一布里淵區中所有能量本徵態的集合構成了電子的能帶結構。在單電子近似的框架內，周期性勢場中電子運動的巨觀性質都可以根據能帶結構及相應的波函式計算出。
上述結果的一個推論為：在確定的完整晶體結構中，布洛赫波矢k是一個守恆量（以倒易點陣矢量為模），即電子波的群速度為守恆量。換言之，在完整晶體中，電子運動可以不被格點散射地傳播（所以該模型又稱為近自由電子近似），晶態導體的電阻僅僅來自那些破壞了勢場周期性的晶體缺陷。
從薛丁格方程出發可以證明，哈密頓算符（Hamiltonian）與平移算符（translation）的作用次序滿足交換律，所以周期勢場中粒子的本徵波函式總是可以寫成布洛赫函式的形式。更廣義地說，本徵函式滿足的算符作用對稱關係是群論中表示理論的一個特例。
布洛赫波的概念由菲利克斯·布洛赫在1928年研究晶態固體的導電性時首次提出的，但其數學基礎在歷史上卻曾由喬治·威廉·希爾（George William Hill，1877年），加斯東·弗洛凱（Gaston Floquet，1883年）和亞歷山大·李雅普諾夫（Alexander Lyapunov，1892年）等獨立地提出。因此，類似性質的概念在各個領域有著不同的名稱：常微分方程理論中稱為弗洛凱理論（也有人稱“李雅普諾夫-弗洛凱定理”）；一維周期性波動方程則有時被稱為希爾方程（Hill's equation）。