簡介
中文名稱：倒格子
英文名稱：Reciprocal Lattice
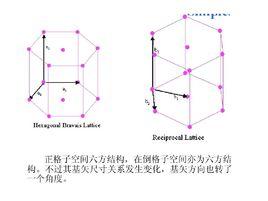
倒格子，亦稱倒易格子(點陣)，它在固體物理學中，特別是在晶格動力學理論、晶體電子論以及晶體衍射方面有著較為廣泛的套用。
定義
假定晶格點陣基矢 a1、 a2、 a3（1、2、3表示 a 的下標，粗體字表示 a1 是矢量，以下類同）定義一個空間點陣，我們稱之為正點陣或正格子，若定義
b1 = 2 π ( a2 × a3) / ν
b2 = 2 π ( a3 × a1) / ν
b3 = 2 π ( a1 × a2) / ν
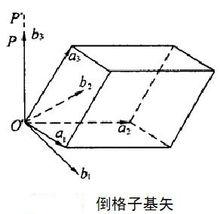倒格子其中 v = a1 · ( a2 × a3 ) 為正點陣原胞的體積，新的點陣的基矢 b1、 b2、 b3是不共面的，因而由 b1、 b2、 b3也可以構成一個新的點陣，我們稱之為 倒格子 ，而 b1、 b2、 b3 稱為 倒格子基矢。
性質
1. 倒格子的一個矢量是和晶格原胞中一組晶面相對應的，它的方向是該晶面的法線方向，而它的大小則為該晶面族面間距倒數的2π倍。
2. 由倒格子的定義，不難得到下面的關係
a· b = 2 π δ
證明正交（垂直）3. 設三維倒格子與正點陣（格子）中的位置矢量分別為
G = α b1+ β b2 + γ b3 R = η a1 + θ a2 + λ a3 (α,η,β,θ,γ,λ皆為整數)
不難證明 G·R = 2π ( αη + βθ +γλ ) = 2π n，其中n為整數。
4. 設三維倒格子原胞體積為 ψ ，正格子原胞體積為 v ，根據倒格子基矢的定義，並利用矢量乘法運算知識，則可得到 ψ v = ( 2 π )^3.
5. 正格子晶面族(αβγ)與倒格子矢量 G = α b1+ β b2 + γ b3 正交
6.正格子與倒格子的體積互為倒數
證明體積互為倒數倒格子引入的意義
這裡簡單的說一點，如上面的性質1，倒格子中的一個基矢對應於正格子中的一族晶面，也就是說，晶格中的一族晶面可以轉化為倒格子中的一個點，這在處理晶格的問題上有很大的意義。例如，晶體的衍射是由於某種波和晶格互相作用，與一族晶面發生干涉的結果，並在照片上得出一點，所以，利用倒格子來描述晶格衍射的問題是極為直觀和簡便的。
另外，在固體物理中比較重要的 布里淵區 ，也是在倒格子下定義的。
