弗洛凱定理
考慮微分方程X'(t)=A(t)X(t),
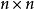 弗洛凱理論
弗洛凱理論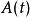 弗洛凱理論
弗洛凱理論 弗洛凱理論
弗洛凱理論其中, 矩陣 是一周期為 的連續周期函式。
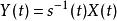 弗洛凱理論
弗洛凱理論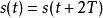 弗洛凱理論
弗洛凱理論弗洛凱理論的主要定理-弗洛凱定理給出了一般線性系統的每個基本解的正規形式。它給定了一座標變換 ,其中 ,用以來轉變周期系統至有常數及實係數的傳統線性系統。
在固態物理中,其類比的結果(推廣至三維)為布洛赫定理。
證明
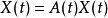 弗洛凱理論
弗洛凱理論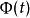 弗洛凱理論
弗洛凱理論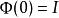 弗洛凱理論
弗洛凱理論 弗洛凱理論
弗洛凱理論由線性微分方程組的基本理論,方程 有一個基解矩陣 ,滿足 ,其中 是單位矩陣。
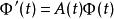 弗洛凱理論
弗洛凱理論從關係式 ,容易看出,
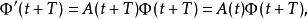 弗洛凱理論
弗洛凱理論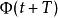 弗洛凱理論
弗洛凱理論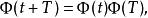 弗洛凱理論
弗洛凱理論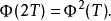 弗洛凱理論
弗洛凱理論故 也是一個基解矩陣。由線性微分方程組的基本理論,必然有同時還能得到
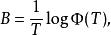 弗洛凱理論
弗洛凱理論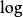 弗洛凱理論
弗洛凱理論 弗洛凱理論
弗洛凱理論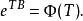 弗洛凱理論
弗洛凱理論定義其中 是矩陣對數(很可能不是實矩陣)。那么設
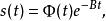 弗洛凱理論
弗洛凱理論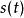 弗洛凱理論
弗洛凱理論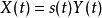 弗洛凱理論
弗洛凱理論可知非退化,設並帶入原方程,通過一系列化簡可以得到
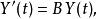 弗洛凱理論
弗洛凱理論這是一個常係數線性微分方程。
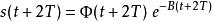 弗洛凱理論
弗洛凱理論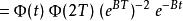 弗洛凱理論
弗洛凱理論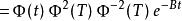 弗洛凱理論
弗洛凱理論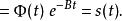 弗洛凱理論
弗洛凱理論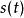 弗洛凱理論
弗洛凱理論故也是周期的。
套用
 弗洛凱理論
弗洛凱理論 弗洛凱理論
弗洛凱理論量子力學中,含時薛丁格方程為。 如果哈密頓量滿足周期性邊界條件, ,可以假定含時薛丁格方程的解為,其中,應滿足。 則原含時薛丁格方程變換為一個新的類似定態的薛丁格方程其中為新的Floquet哈密頓量, 為準能量,被稱為Floquet態。
