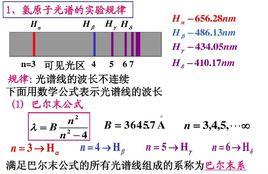
定義
巴耳末公式是1885年由瑞士數學教師巴耳末提出的用於表示氫原子譜線波長的經驗公式
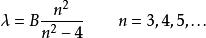 巴爾末公式
巴爾末公式其中 B 是一個常數,其值為B=3.6546×10 m
此外該公式還有一個用里德伯常數改寫的版本,如下:
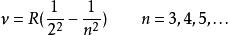 巴爾末公式
巴爾末公式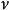 巴爾末公式
巴爾末公式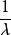 巴爾末公式
巴爾末公式或者將用表示:
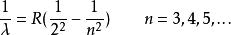 巴爾末公式
巴爾末公式其中R是里德伯(Rydberg)常數,其值為1.0973731569×10 m
歷程
巴耳末公式的提出經歷了一個曲折的過程。在巴塞爾大學兼任講師期間,年近60歲的巴耳末受到該校一位研究光譜的物理學教授哈根拜希(E.Hagenbach)的鼓勵,開始試圖尋找氫原子光譜的規律。當時氫光譜見光區波段的4條譜線已經過埃姆斯特朗等人的精確測定,通過觀測恆星光譜也發現了紫外波段的10條譜線,然而它們波長的規律尚不為人所知。巴耳末從尋找可見光波段4條譜線波長的公共因子和比例係數入手,否定了將譜線類比聲音的思路。受投影幾何的啟發,巴耳末利用幾何圖形為這些譜線的波長確定了一個公共因子,寫出了巴耳末公式。巴耳末公式計算出的波長與實際測量值的誤差不超過波長的1/40000,吻合得非常好。隨後巴耳末又繼續推算出當時已發現的氫原子全部14條譜線的波長,結果和實驗值完全符合。1884年6月25日,巴耳末在巴斯勒自然科學協會的演講中公布了這個公式,同年又將其發表在當地一個刊物上,1885年又刊載在《物理、化學紀要》雜誌上。幾年後,巴耳末又發表了有關氦光譜和鋰光譜的各譜線頻率之間的類似關係。
產生的影響
巴爾末公式對光譜學和近代原子物理學的發展產生了重要影響。用巴爾末公式表達的一組譜線位於可見光區,為紀念巴爾末,人們把這組譜線系命名為巴耳末系。隨後又發現了不同於巴爾末系的賴曼系、帕刑系等線系,它們都符合比巴爾末公式更為普遍的里德伯公式。
巴耳末系
巴耳末系或 巴耳末線是原子物理學中氫原子六個發射譜線系列之一的名稱。
巴耳末系的計算可以使用約翰·巴耳末在1885年發現的 巴耳末公式- 一個經驗式。 來自氫原子所發射的光譜線在可見光有4個波長:410奈米、434奈米、486奈米和656奈米。它們是吸收光子能量的電子進入受激態後,返回主量子數 n等於2的量子狀態時釋放出的譜線。
巴耳末系在天文學中特別有用,因為巴耳末線出現在許多天體的現象中。而且氫在宇宙中的豐盈度,使它在被看見時,總是比共同存在的其他元素譜線更為顯而易見。
在恆星的光譜類型,主要是由表面的溫度決定,是建立在光譜線的相對強度上,而巴耳末系在這方面室非常重要的。其它可以取決於進一步光譜分系的特徵還包括表面重力(與物體的大小有關)和成分(結構)。 . 因為在各種不同的天體中巴耳末系都是可以觀察到的譜線,它們常被利用都卜勒位移來測量視線速度。這在天文學所有的領域上都很有用,像是測量聯星、系外行星、中子星和黑洞等緻密天體(測量圍繞著的吸積盤中氫的運動)、確認有著相似運動天體的起源和是否是同一群天體(移動星群、星團、星系團、和來自碰撞的碎片)、測量星系或類星體的距離(精確的紅移)、或是經由光譜分析辨識出不熟悉的天體。
依據被觀測對象的本質,巴耳末線可以出現在吸收譜線或發射譜線中。在恆星,巴耳末系通常是吸收線,而且在表面溫度10,000K(光譜類型A)的恆星最為強烈(明顯)。在許多的不規則星系、螺旋星系、AGN、HII區、和行星狀星雲,巴耳末線是發射線。
在恆星光譜中,H-ε線(7躍遷至2)經常會與其他的吸收譜線混合,天文學家都知道電離的鈣的"H"(夫朗荷斐譜線中的標示),CaH的波長是396.847奈米,與H-ε線非常接近,在低解析的光譜中式無法分辨兩者的。同樣的,H-ζ線(8躍遷至2)在高溫恆星中也會與中性氦的混合。
參閱
•巴耳末系
•里德伯公式
•玻爾模型