介紹
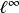 巴拿赫極限
巴拿赫極限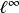 巴拿赫極限
巴拿赫極限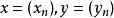 巴拿赫極限
巴拿赫極限 巴拿赫極限
巴拿赫極限在數學分析中, 巴拿赫極限(英語:Banach limit)指的是定義在全體有界復序列組成的巴拿赫空間上,對每個 中的序列 和複數 滿足:
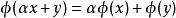 巴拿赫極限
巴拿赫極限(1) (線性);
 巴拿赫極限
巴拿赫極限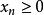 巴拿赫極限
巴拿赫極限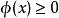 巴拿赫極限
巴拿赫極限(2)若對每個 有 ,則 (正定性);
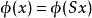 巴拿赫極限
巴拿赫極限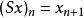 巴拿赫極限
巴拿赫極限(3) ,其中S是移位運算元,定義為 (移位不變性);
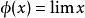 巴拿赫極限
巴拿赫極限(4)若x是收斂序列,則 .
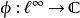 巴拿赫極限
巴拿赫極限的連續線性泛函。
 巴拿赫極限
巴拿赫極限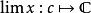 巴拿赫極限
巴拿赫極限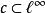 巴拿赫極限
巴拿赫極限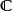 巴拿赫極限
巴拿赫極限因此, 是對連續線性泛函 的延拓,其中 是 中收斂到某個極限的全體序列組成的復向量空間。進而可以視為發散級數論中的一個可和法。
換句話說,巴拿赫極限是對通常意義下極限概念的延拓,並且是線性、移位不變、正定的。可以對某個序列找到兩個巴拿赫極限,使得各自作用下得到兩個不同的值,我們稱這類序列的巴拿赫極限不是唯一確定的。
作為上述性質的一個推論,每個實值巴拿赫極限也滿足:
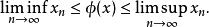 巴拿赫極限
巴拿赫極限巴拿赫極限的存在性通常需要套用哈恩-巴拿赫定理證明(分析學方法),也可以套用超濾子(這種方法在集合論的討論中出現得更頻繁)。這些證明都一定會用到選擇公理(即所謂的非構造證明)。
幾乎收斂
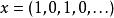 巴拿赫極限
巴拿赫極限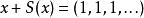 巴拿赫極限
巴拿赫極限某些不收斂的級數在巴拿赫極限的作用下是唯一確定的。 例如 ,注意到 是常序列,並且
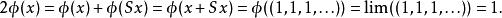 巴拿赫極限
巴拿赫極限因此對每個巴拿赫極限而言,它以1/2為極限。
 巴拿赫極限
巴拿赫極限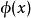 巴拿赫極限
巴拿赫極限我們將每個巴拿赫極限 下有相同的 的有界序列 x稱為幾乎收斂的。
Ba 空間
 巴拿赫極限
巴拿赫極限 巴拿赫極限
巴拿赫極限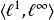 巴拿赫極限
巴拿赫極限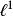 巴拿赫極限
巴拿赫極限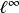 巴拿赫極限
巴拿赫極限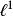 巴拿赫極限
巴拿赫極限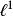 巴拿赫極限
巴拿赫極限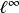 巴拿赫極限
巴拿赫極限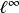 巴拿赫極限
巴拿赫極限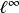 巴拿赫極限
巴拿赫極限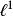 巴拿赫極限
巴拿赫極限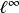 巴拿赫極限
巴拿赫極限在 中給定收斂序列 ,如果考慮對偶 ,x通常的極限並不由的某個元素給出。實際上是的連續對偶空間(對偶巴拿赫空間);反過來,雖然能誘導出中的連續線性泛函,但並不是全部。每個上的巴拿赫極限都是的對偶巴拿赫空間中的一個元素,但不在中。的對偶叫做ba空間,由一切自然數集子集的σ-代數上有限可加(符號)測度組成,或者等價地說是由每個自然數集的Stone–Čech緊化上的波萊爾(符號)測度組成。
