基本介紹
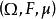 博赫納積分
博赫納積分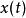 博赫納積分
博赫納積分設 是完備的σ有限測度空間, 是定義在Ω上而取值於巴拿赫空間X的向量值函式:
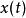 博赫納積分
博赫納積分1.若 是Ω上的可數值函式,即
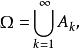 博赫納積分
博赫納積分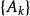 博赫納積分
博赫納積分而 是Ω中一列互不相交的可測集,
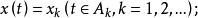 博赫納積分
博赫納積分又
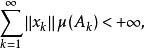 博赫納積分
博赫納積分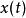 博赫納積分
博赫納積分則稱 在Ω上是博赫納可積的,並稱
 博赫納積分
博赫納積分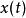 博赫納積分
博赫納積分為 的博赫納積分,記為
 博赫納積分
博赫納積分即
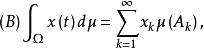 博赫納積分
博赫納積分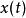 博赫納積分
博赫納積分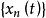 博赫納積分
博赫納積分2.對於一般的強可測函式 ,若它是博赫納可積的可數值函式列 的關於μ幾乎處處強收斂的極限且
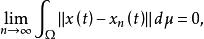 博赫納積分
博赫納積分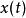 博赫納積分
博赫納積分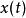 博赫納積分
博赫納積分則說 在Ω上是博赫納可積的,並規定 的博赫納積分為
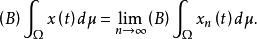 博赫納積分
博赫納積分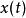 博赫納積分
博赫納積分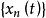 博赫納積分
博赫納積分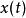 博赫納積分
博赫納積分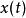 博赫納積分
博赫納積分對於博赫納可積函式 ,它的積分值(向量)不依賴於 的選取,博赫納積分是勒貝格積分在向量值函式情形的直接推廣,是由博赫納(S.Bochner)在1932年建立的,這種積分在向量值測度理論、運算元理論、機率論、隨機過程以及巴拿赫空間幾何理論等許多數學分支中有廣泛的套用,向量值函式 為博赫納可積的充分必要條件是 強可測,且
 博赫納積分
博赫納積分博赫納積分具有和勒貝格積分類似的若干基本性質,例如,具有線性性、完全可加性、絕對連續性以及控制收斂定理、富比尼定理均成立,但拉東-尼科迪姆定理不成立,就是說,與通常的抽象測度不同,絕對連續的向量值測度不一定能表示成博赫納積分 。
集值映射的積分
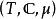 博赫納積分
博赫納積分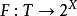 博赫納積分
博赫納積分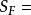 博赫納積分
博赫納積分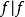 博赫納積分
博赫納積分 博赫納積分
博赫納積分集值映射的積分(integral of setvalued mapping)是單值映射的積分到集值映射情形的推廣,集值映射有多種可積性概念。設 是測度空間,X是可分巴拿赫空間, 是具非空緊凸值的可測集值映射,記 { 是F的可測單值選擇}。若 為佩蒂斯可積(相應地,博赫納可積),則稱F為佩蒂斯可積(相應地,博赫納可積),且其積分定義為
 博赫納積分
博赫納積分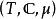 博赫納積分
博赫納積分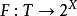 博赫納積分
博赫納積分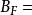 博赫納積分
博赫納積分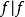 博赫納積分
博赫納積分 博赫納積分
博赫納積分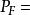 博赫納積分
博赫納積分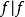 博赫納積分
博赫納積分 博赫納積分
博赫納積分集值映射的積分現有多種不同的概念。例如,還有下述集值映射的積分概念。設 是測度空間,X是可分巴拿赫空間, 是具非空閉值的可測集值映射.記 { 是F的可測單值選擇,且 在T上為博赫納可積}與 { 是F的可測單值選擇,且 在T上為佩蒂斯可積},集值映射F在T上的博赫納積分與佩蒂斯積分分別定義為
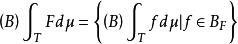 博赫納積分
博赫納積分與
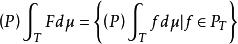 博赫納積分
博赫納積分其中
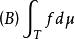 博赫納積分
博赫納積分與
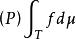 博赫納積分
博赫納積分分別表示f在T上的博赫納積分與佩蒂斯積分。
博赫納
博赫納(1899-1982,Bochner,Salomon)是美國數學家。1899年8月20日生於奧匈帝國的克拉科夫(現屬波蘭);1982年5月2 日卒於美國休斯頓。就學於柏林大學,1921年獲博士學位。1924-1926年在哥本哈根大學、劍橋大學、牛津大學邊學習邊工作。1927-1933 年任慕尼黑大學講師。1933 年到美國普林斯頓大學任副教授,1938 年人美國籍,1946 年晉升為教授,1968 年退休。1968年以後任賴斯大學教授,並任數學系系主任多年。1950年被選為美國全國科學院院士。1957-1958 年任美國數學會副主席。
博赫納在機率論、傅立葉分析、多複變函數、調和分析、複流形、復變及概周期函式等領域都有貢獻。
20世紀20 年代初,H·玻爾給出了一類概周期函式,但取和方法相當複雜,博赫納很快就建議玻爾採用簡單許多的博赫納-費耶爾過程。博赫納還用拓撲緊緻性性質使玻爾函式特徵化,後來馮·諾伊曼用此把概周期函式從歐氏空間推廣到了一般群。1932 年他又給出了博赫納積分,即巴拿赫空間元素的函式的勒貝格積分;並很快引入了玻爾函式的相應推 廣一“抽 象” 概 周 期 函 數。1961年博赫納又引人了比玻爾函式更一般的概自守函式。
 博赫納積分
博赫納積分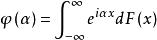 博赫納積分
博赫納積分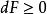 博赫納積分
博赫納積分 博赫納積分
博赫納積分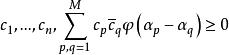 博赫納積分
博赫納積分博赫納在1932 年給出了博赫納正定函式定理,即連續復值函式能表示成傅立葉-斯蒂爾傑斯積分,其中,若且唯若對任意有限點,,和復常數時才成立。這一判別準則在機率論中有不少套用,而且還可套用於希爾伯特空間自伴運算元譜表示的推導中,並已被推廣運用到了拓撲群空間的函式。
博赫納是施瓦爾茨廣義函式理論的先驅者。他引入了函式的廣義傅立葉變換。1936年,他還首先引入了多重傅立葉級數的球形和,現已成為多重傅立葉展開的收斂問題和逼近問題的重要工具。
在多複變函數領域,1943年他用“博赫納-馬丁內利核”證明了“對於具連通邊界的有界域,邊界上的全純函式可以延拓到該域的整個內部”這一哈托格斯的關鍵性定理。1938年,他證明了管的正則包絡也是管,包絡管的基是原來管的基的凸閉包。
在機率論領域,博赫納在1946年引入了一類一般形式的隨機過程的傅立葉變換,把加性集函式隨機化,不僅得到三維納微分空間,而且還得到了同類型的其他平穩過程。
博赫納因對機率論、傅立葉分析、多複變函數等領域的貢獻及影響,而於1979 年獲美國數學會的斯蒂爾獎。他著有《多復變數》(Several ComplexVariables,1948;與W.T.馬丁合作)、《調和分析與機率論》(Harmonic Analysis andtheTheory of Probability,1956)、《曲率和貝蒂數》(Curvatureand Betti Numbers,1953;與 矢野健太郎合作)和《傅立葉積分》(Fourier Integrals,1959) 等書 。

