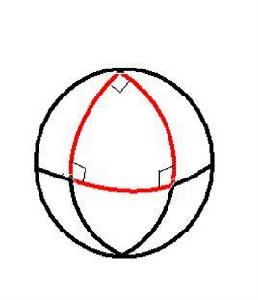
球面三角形
球面三角是研究球面三角形的邊、角關係的一門學科。從十六世紀起由於天文學、航海學、測量學等方面的發展,球面三角逐漸形成了獨立學科。從平面三角學我們知道,一圓周的1/360 ,叫做1度的弧。1度弧的1/60 叫做1角分的弧。1角分弧的1/60 叫做1角秒的弧。根據弧和所對圓心角的關係,可以得出角的量度。一圓周所對的圓心角為360°。因此,1度的弧所對的圓心角,叫做1°的角;1角分的弧相對的圓心角,叫做1′;1角秒的弧所對的圓心角,叫做1‘’。
球面三角形的基本概念
球面上的圓:一個過球心的平面和球面相截的截痕稱為球面上的大圓;一個不過球心的平面和球面相截的截痕稱為球面上的小圓。過球面上不在同一直徑兩端的任意兩點,只能作一個大圓,卻能作無數個小圓。
球面距離:球面上兩點間小於180°的大圓弧(劣弧)長稱為球面距離,以大圓弧所對應的球心角用度、分、秒來度量。可以證明,球面上兩點間的最近距離就是過球面上兩定點間小於180°的大圓弧(劣弧)。
極、極線、極距:垂直於任一圓面(大圓和小圓)的球直徑稱為該圓的軸。軸與球面相交的兩點稱為極。球上每一個圓均有兩個極。從大圓弧或小圓弧上的一點到極的球面角距稱為極距。顯然,同圓上任一點的極距都相等。大圓的極距等於90°。極距等於90°的大圓弧稱為極線或稱為赤道。
球面角:球面上一點及過該點的任意兩條大圓弧所構成的圖形稱為球面角,該點稱為球面角的頂點,這兩條大圓弧稱為球面角的邊。球面角的大小由過頂點的兩個大圓弧平面所構成的二面角來確定。
對稱球面三角形簡介
對稱球面三角形(symmetrical spherical triangles)是兩個位置相關的球面三角形,它指具有對稱性質的兩個球面三角形。對稱球面三角形分兩種類型:
1,關於球心成中心對稱,即對心球面三角形。
2,關於某大圓對稱(在空間,關於過球心的平面對稱)。
此時,兩球面三角形的對應元素相等,但兩球面三角形的定向相反。
性質
對稱,指物體或圖形在某種變換條件(例如繞直線的旋轉、對於平面的反映,等等)下,其相同部分間有規律重複的現象,亦即在一定變換條件下的不變現象。
因此,與平面對稱三角形類似,把一個圖形繞著某一點旋轉 ,如果它能夠與另一個圖形重合,那么就說這兩個圖形關於這個點對稱,這個點叫做對稱中心,兩個圖形關於點對稱也稱中心對稱,這兩個圖形中的對應點,叫做關於中心的對稱點。中心對稱的兩個圖形具有如下性質:(1)關於中心對稱的兩個圖形全等;(2)關於中心對稱的兩個圖形,對稱點的連線都過對稱中心,並且被對稱中心平分。