基本介紹
如果△ABC三邊BC,CA,AB與一直線各交於D,E,F(其中有一點是外分點,或三點都是外分點),則
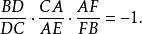 門納勞斯定理
門納勞斯定理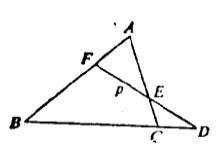 圖1
圖1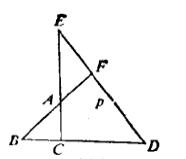 圖2
圖2詳細介紹
門納勞斯(Menelaus) 是三角學的奠基者。托勒密在《天文學大成》中記載了門納勞斯的兩次天文觀測,時間在公元98年。普魯塔克在書中描述門納勞斯和人談話,時間約當75年以後,地點在羅馬或其附近。帕波斯和普魯塔克都稱他為亞歷山大的門納勞斯。由此可知門納勞斯在公元100年前後活動於亞歷山大及羅馬。托勒密所記載的兩次觀測,一次是月亮掩(occultation) 角宿一(Spica, 室女座α),另一次是對比古代的記錄,門納勞斯再度證實希帕霍斯發現的歲差現象的存在 。
在阿拉伯學者伊本 納迪姆(Ibn al-Nadim,10 世紀下半葉)的《數學家名錄》中列舉了門納勞斯的幾種著作,但現在只有《球面學》(Sphaerica) 一種以阿拉伯文譯本的形式流傳下來,其餘的均已失傳。譯者是伊沙格(Is hāq ibn Hunain, 910年卒)或他的父親胡奈因(Hunain ibn Ishāq, 877年卒)。以後有幾種修訂本,現藏在萊頓大學圖書館。
當前較完整的現代語版本是布約恩博(Axel Anthon Björnbo)的德文譯本(1902),以後又有克勞澤(Max Krause)的德文修訂增補本。這是研究門納勞斯的兩種基本文獻 。
《球面學》是廣j納勞斯的精心傑作,因此書中門納勞斯被尊稱為“三角學的奠基者”,而且是第一個使三角學脫離天文學,成為獨立學科的人。
全書共3卷,卷Ⅰ開宗明義就給出球面三角形的定義:“在球面上由大圓弧所包圍的部分”,又限定“這些弧都小於半圓”。這是世界上第一次對球面三角形的明確表達。寫作的體例雖然仍遵循希臘的傳統,但不拘泥於從最原始的定義出發,如球面上的點、極點、小圓、大圓等,而是直截了當指明要討論的對象。前人已給出的概念和命題,此處作為已知來使用。
根據帕波斯的記載,門納勞斯稱球面三角形為“三邊形”(three-side),以區別於平面幾何中的三角形(triangle)。按阿拉伯文版本,他在獻給某一位王子時宣稱:“我發現了一種極好的推理證明方法。”這是可信的,球面三角的許多重要內容,都是門納勞斯的獨創。
卷Ⅰ的主要內容是比較球面與平面這兩種三角形的異同,力圖平行於歐幾里得《幾何原本》,建立相等的球面三角形命題。他儘量採用直接證法而避免用歸謬法,有些命題的證明及討論比《原本》更全面,因為《原本》中某些情形是有意留給讀者自證的。
他給出與平面三角形類似的若干命題之後,也指出兩者的差異。如球面三角形三內角之和並不等於兩直角而是大於兩直角。兩平面三角形如各角對應相等只是相似而不一定全等,但兩個球面三角形若各角相等則必定全等(或對稱)。這是球面同平面明顯的區別。
卷Ⅰ沒有多少新鮮的內容,只是建立一些對天文學有用的命題,一般不超出西奧多修斯(Theodosius of Bithynia,公元前2世紀下半葉)《球面學》(Sphaerica)的範圍,有些是加以推廣,證明通常是冗長的。
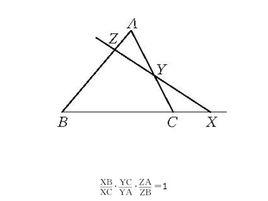
卷Ⅰ、卷Ⅱ只牽涉到球面幾何,卷Ⅲ才正式開展球面三角學的論述。第1個命題就是球面的“ 門納勞斯定理”。現今在平面幾何及射影幾何中有平面的“門納勞斯定理”,一般表述為:設X,Y,Z分別是△ABC三條邊BC,CA,AB或其延長線上的點,則此三角形共線的充要條件是(圖3) :
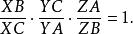 門納勞斯定理
門納勞斯定理 圖3
圖3這命題不是門納勞斯的發明,前人早已知道,它也許載在歐幾里得已失傳的《推論集》(Porisms)中。門納勞斯在這裡是作為已知來使用的。他自己所證明的是這命題在球面上的推廣:設X,Y,Z分別是球面三角形ABC三條邊BC,CA,AB或其延長線上的點,則此三點共大圓的充要條件是(圖4):
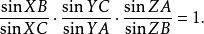 門納勞斯定理
門納勞斯定理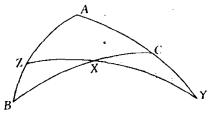 圖4
圖4以上是用現代的術語和符號來表達的,當時還沒有三角函式,只有希帕霍斯的弦表,就是不同圓心角所對弦長的表,相當於現在圓心角之半的正弦線的兩倍。門納勞斯大概也造過這樣的表。他用弦長來表示前面的關係式,實質上和正弦一樣。
這定理稱為“ 門納勞斯定理”是名正言順的,由於平面的情形不知出處,後人就一併稱之為“門納勞斯定理”。它的另一種提法(平面情形)是:設一直線與三角形的三條邊或其延長線相交,將三條邊分(內分或外分)為六條線段,則三條沒有公共端點的線段之積,等於另外三條線段之積。球面情形也有類似的說法,因為關係到六個量,在中世紀時常稱為“六量律”(regula sex quantitatum)。在托勒密《天文學大成》中對平面及球面的情形都作了詳細的證明 。
門納勞斯從這個定理導出很多有用的結果。如命題2證明了兩個球面三角形ABC與A'B'C,若A=A',C=C(或C與C互補),則
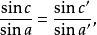 門納勞斯定理
門納勞斯定理(依習慣,A,B,C角所對的邊分別記作a,b,c)特別是C與C'都是直角時,後來被稱為“四量律”(regula quattuor quantitatum),在阿拉伯三角學中占有重要的地位。
命題5證明:若球面三角形ABC及A'B'C'的C,C'是直角,B=B',又a,a' 都小於90°,則
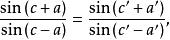 門納勞斯定理
門納勞斯定理可以由此導出
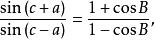 門納勞斯定理
門納勞斯定理它等價於cosB=tga ctgc。這是解球面直角三角的基本公式之一。
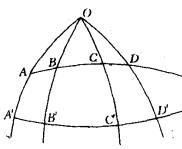 圖5
圖5在證明上述命題的過程中,門納勞斯套用了非調和比(交比)的性質(圖5):通過O點有4條大圓弧OAA',OBB',OCC',ODD',被任意兩條大圓弧ABCD,A'B'C'D'所截,則
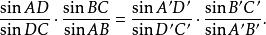 門納勞斯定理
門納勞斯定理在平面上,有這樣的定理:過一點的4條直線與任一截線的4個交點的非調和比(即交比)與該截線的位置無關。推廣於球面就有上面的關係,只要將直線變成大圓弧,線段變成圓弧的正弦即可。
還有好幾個可以和平面類比的命題。如命題6:平分球面三角形ABC頂角,A的大圓弧交BC於D,則
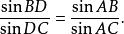 門納勞斯定理
門納勞斯定理命題11以後,又轉到和天文有關的問題上去。以最後的命題15第一部分為例(圖6):
 圖6
圖6設BA,BC是大圓弧的一個象限,P是BA的極點。PA₂,PA₁是過P點的象限弧,交BC於C,C₁,R是球半徑,r,r₁,r₂分別是過C,C₁,C₂三點的小圓(平行於大圓A'BA)半徑,則
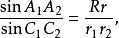 門納勞斯定理
門納勞斯定理這公式自然可以用來解決天球上各種圈(如赤道、黃道、白道等)之間的關係。
可以肯定,門納勞斯已經掌握了球面三角學的基本原理。此外,他還研究過力學問題(據阿拉伯文獻),寫過《幾何原理》,發現一種“奇特曲線”(the paradoxical curve),但都已失傳 。