概念
1、在數學上,兩個圖形可以完全重合,或者說兩個物體形狀相同、大小相等,那么這兩個圖形全等。“全等”用符號“≌”表示,讀作“全等於”。(例:△ABC≌△A‘B’C‘,讀作三角形ABC全等於三角形A‘B’C’)
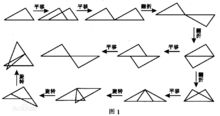
2、一個圖形經過翻折、平移和鏇轉變換所得到的新圖形一定與原圖形全等。反過來,兩個全等的圖形經過上述變換後一定可以互相重合。
3、兩個多邊形全等,互相重合的頂點叫對應頂點,互相重合的邊叫對應邊,互相重合角的叫對應角。
性質
 全等三角形
全等三角形在數學中,全等一般是指全等三角形。全等三角形是指兩個形狀相同、大小相等的三角形。全等三角形的對應角相等、對應邊相等。
注意:
1)性質中三角形全等是條件,結論是對應角、對應邊相等。而全等的判定卻剛好相反;
2)利用性質和判定,學會準確地找出兩個全等三角形中的對應邊與對應角是關鍵。在描述兩個三角形全等時,一定把對應的頂點,角、邊的順序寫一致,為找對應邊,角提供方便。
判定
平面三角形
判定公理
(1)有兩邊及其夾角對應相等的兩個三角形全等“邊角邊”簡稱“SAS” ;
(2)有兩角及其夾邊對應相等的兩個三角形全等“角邊角”簡稱“ASA”;
(3) 三組對應邊分別相等的兩個三角形全等“邊邊邊”簡稱“SSS”;
(4)有兩角及其一角的對邊對應相等的兩個三角形全等“角角邊”簡稱“AAS”;
(5)直角三角形全等條件有:斜邊及一直角邊對應相等的兩個直角三角形全等“斜邊、直角邊”簡稱“HL”(直角三角形);
常見誤區
在全等的判定中,沒有AAA和SSA,這兩種情況都不能唯一確定三角形的形狀。
SSA “邊邊角”,有三種情況可證明此三角形全等:
1.相等的角為鈍角
2.相等的角為直角.
3.相等的角的對邊最長
球面三角形
以下均指在同球面或等球面中的兩個球面三角形:
如果球面三角形的三個邊分別對應相等,則兩個球面三角形分別對應相等(SSS);
如果球面三角形的兩邊與它們的夾角分別對應相等,則兩個球面三角形全等(SAS);
如果球面三角形的兩角與它們的夾邊分別對應相等,則兩個球面三角形全等(ASA) ;
如果球面三角形的三個角分別對應相等,則兩個球面三角形分別對應相等(AAA);
對球面三角形而言,AAS不成立,因為內角和是個不定值。
