概念
對偶映射(dual mapping)是線性代數中共軛變換的推廣。設E*,E與F*,F是對偶空間,φ是E到F的線性映射,φ*是F*到E*的線性映射。若對任意x∈E,y*∈F*,有:
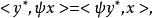 對偶映射
對偶映射則稱φ與φ*是一對對偶映射。設φ是E到F的線性映射,若φ的對偶映射存在,則是惟一的。若E是有限維的,則φ的對偶映射是存在的,因而是惟一的。設E*與E,F*與F(i=1,2)是對偶的向量空間,φ是E→E,ψ是F→F的線性映射。若φ*與ψ*存在,則:
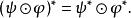 對偶映射
對偶映射性質
由對偶關係確定的從巴拿赫空間到其對偶空間的集值映射。設X是巴拿赫空間,X為其對偶空間。設μ是一個規範函式,即μ:[0,+∞)→[0,+∞)滿足條件:μ(0)=0,μ嚴格遞增,
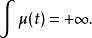 對偶映射
對偶映射定義集值映射J:X→2 為:
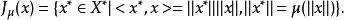 對偶映射
對偶映射這樣定義的集值映射J稱為是以μ為規範函式的對偶映射。μ(t)=t時對偶映射J稱為標準對偶映射。對偶映射是齊次的,此外有下述結論:
1.J為滿值⇔X是自反的。
2.J為嚴格單調⇔X是嚴格凸的。
3.J為單值映射⇔X是光滑的。
4.J為線性運算元⇔X是希爾伯特空間。
對於自反巴拿赫空間,總可取X中的等價範數使得X和X都是嚴格凸的,此時J:X→X是單值、嚴格單調、有界滿值、次連續的(S)型映射。
共軛變換
亦稱轉置變換。一種重要的線性變換。設V是域P上的線性空間,J是P的對合自同構(即J=J ),φ是V上的非退化埃爾米特(反埃爾米特)函式,σ是V的線性變換.若存在V的線性變換σ*,使對V中任二向量α,β滿足條件φ(σ(α),β)=φ(α,σ*(β)),則稱σ*為σ的共軛變換;若σσ*=σ*σ,則稱σ為正規變換;若σ=σ*(-σ*),則稱σ為自共軛(反自共軛)變換,或埃爾米特(反埃爾米特)變換;若J是P的自同構,則φ為V上的非退化對稱(反對稱)雙線性型。此時V的自共軛(反自共軛)變換,亦稱為對稱(反對稱)變換。
對偶空間
對偶空間是一種特殊的線性空間。即線性空間的線性函式空間。設V是域P上的線性空間,V的所有線性函式構成的域P上的線性空間,稱為V的對偶空間,記為V(即Hom(V,P))。當dim V=n,並且ε,ε,…,ε是V的基時,由等式ε*(ε)=δ(i,j=1,2,…,n)所確定的n個線性函式ε,ε,…,ε是V的基,稱為基ε,ε,…,ε的對偶基。由上知,當dim V=n有限時,dim V*=dim V=n;但當dim V無限時,二者不再相等,即它們的基元素不再是一一對應的。
線性映射
亦稱同態或線性同態。線性代數的中心內容和基本概念之一。是同一域上兩個線性空間V與W之間具有線性性質的映射,即V到W的映射φ,若對任意α,β∈V,k∈P,滿足條件:
1.φ(α+β)=φ(α)+φ(β);
2.φ(kα)=kφ(α);
則稱φ為V到W的線性映射,或稱為線性運算元。把V中每一元素映射成W中零元素的映射是線性映射,稱為零映射。若φ是雙射,則稱φ為V與W的線性同構,同時稱φ為線性空間的同構映射。建立了線性同構的兩個線性空間,稱為同構的線性空間。當W=P時,V到P的線性映射也稱為線性函式。
域P上線性空間V到W的全體線性映射的集合,記為Hom(V,W).在Hom(V,W)中可以引入加法與純量乘法,若對任意的φ,ψ∈Hom(V,W),任意α∈V,k∈P,規定:
φ+ψ: (φ+ψ)(α)=φ(α)+ψ(α),
kφ: (kφ)(α)=kφ(α),
則Hom(V,W)構成域P上的線性空間。

