定義
設A為n階實矩陣，如果A =-A，則稱A為實反對稱矩陣。
說明：A 表示轉置矩陣，有時候也記為A'或者A 。
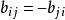實反對稱矩陣若矩陣A滿足條件A=-A ，則稱A為反對稱矩陣。由定義知反對稱矩陣一定是方陣，而且位於主對角線兩側對稱位置上的元素必符號相反，即，其中i、j為任意不大於矩陣維數的實數。
相關定理
實反對稱矩陣有如下性質：
性質1：奇數階反對稱矩陣的行列式值為0。
實反對稱矩陣性質2：當A為n階實反對稱矩陣時，對於有X AX =0。
性質3：實反對稱矩陣的特徵值是零或純虛數。
性質4：若A為實反對稱矩陣，A的特徵值λ= bi(b≠0)所對應特徵向量α+βi中實部與虛部對應的向量α、β相互正交 。
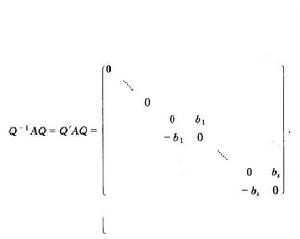
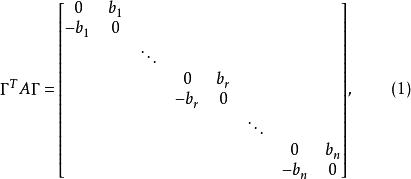
性質5：若A為n階實反對稱矩陣，則存在n階正交矩陣Γ，使得
實反對稱矩陣式中，±ib(k=1，2，…，n)是A的全部非零特徵值。k=1，2，…，r，A的秩r(A)=2r，矩陣(1)稱為實反對稱矩陣A在正交相似下的標準形。
例題解析
【例1】設A為n階反對稱方陣，A*為其伴隨矩陣，證明：當n為奇數時，A*為對稱方陣；當n為偶數時，A*為反對稱方陣。
證明 由於A*中每個元素均為A中的n-1階子式，故對任意數k有
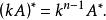實反對稱矩陣又因A'=-A，故可得
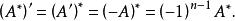實反對稱矩陣
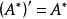實反對稱矩陣
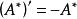實反對稱矩陣當n為奇數時，，即A*為對稱方陣。當n為偶數時，，即A*為反對稱方陣 。
【例2】證明：實反對稱矩陣的特徵根是零或純虛數。
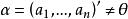實反對稱矩陣證明 設A為實反對稱矩陣，λ是它的任意一個特徵根，而是屬於特徵根λ的一個特徵向量，即
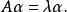實反對稱矩陣一方面，有
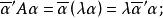實反對稱矩陣另方面，又有
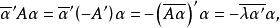實反對稱矩陣故
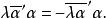實反對稱矩陣但是
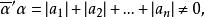實反對稱矩陣故
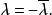實反對稱矩陣即λ為零或純虛數 。
【例3】證明：1)若A，B為同階實對稱矩陣，則AB-BA的特徵根只能是0或純虛數；
2)若A為實反對稱矩陣，則|A+E|≠0。
證明 1)因為A，B都是實對稱矩陣，故：
(AB-BA)'=(AB)'-(BA)'=B'A'-A'B'=BA-AB=-(AB-BA)，
故AB-BA為實反對稱矩陣，由上題知，其特徵根只能是0或純虛數。
2)設若|A+E|=0，則便有|-E-A|=0，這說明A有特徵根-1，這與A是實反對稱矩陣矛盾，故必|A+E|≠0。
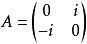實反對稱矩陣注：若A不是實的反對稱矩陣，則結論不成立。例如，是反對稱矩陣，但顯然|A+E|=0 。
