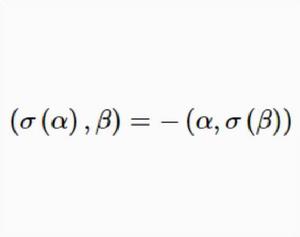基本介紹
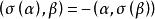 反對稱變換
反對稱變換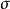 反對稱變換
反對稱變換針對對稱變換,我們把歐氏空間中對任意 ,滿足 的線性變換 叫做反對稱變換。
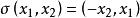 反對稱變換
反對稱變換【例1】在歐氏空間R 中,規定線性變換σ為 ,證明:σ是反對稱變換。
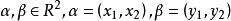 反對稱變換
反對稱變換證明: 因為對任意 ,有:
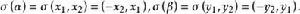 反對稱變換
反對稱變換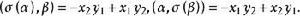 反對稱變換
反對稱變換於是,
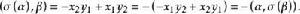 反對稱變換
反對稱變換所以,
故σ是反對稱變換。
反對稱變換的性質
根據反對稱變換的定義,可以證得反對稱變換的以下一些性質:
定理1 歐氏空間V的線性變換σ是反對稱變換的充分必要條件是σ關於V的標準正交基的矩陣是反對稱矩陣。
 反對稱變換
反對稱變換證明 設 是V的組標準正交基,且
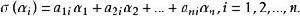 反對稱變換
反對稱變換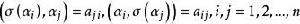 反對稱變換
反對稱變換於是, .
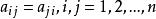 反對稱變換
反對稱變換所以,σ是反對稱變換的充分必要條件是 ,即σ關於V的標準正交基f內矩陣是反對稱矩陣。
性質1 設σ是歐氏空間V的反對稱變換,如果V是σ的不變子空間,則也是σ的不變子空間。
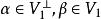 反對稱變換
反對稱變換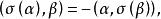 反對稱變換
反對稱變換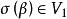 反對稱變換
反對稱變換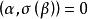 反對稱變換
反對稱變換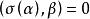 反對稱變換
反對稱變換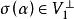 反對稱變換
反對稱變換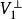 反對稱變換
反對稱變換證明 對任意的向量 ,有 而V是σ的不變子空間,所以 ,故 ,於是得 .因此 ,即 是σ的不變子空間。
性質2 設σ是歐氏空間V的反對稱變換,則σ的特徵根是零或純虛數。
證明 設σ是歐氏空間V的反對稱變換,A是σ關於V的某個標準正交基的
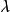 反對稱變換
反對稱變換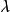 反對稱變換
反對稱變換矩陣, 是A的任一特徵根,α是屬於特徵根 的特徵向量,則有:
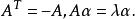 反對稱變換
反對稱變換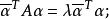 反對稱變換
反對稱變換一方面, 另一方面,有:
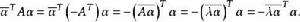 反對稱變換
反對稱變換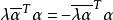 反對稱變換
反對稱變換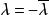 反對稱變換
反對稱變換所以 ,但 ,從而 ,故反對稱實矩陣的特徵根是零或純虛數,即σ的特徵根是零或純虛數。
和對稱變換一樣,因反對稱變換與反對稱矩陣一一對應,所以反對稱變換所具有的性質,反對稱矩陣都具有,這裡從略 。