定義
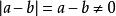 大於
大於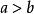 大於
大於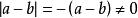 大於
大於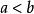 大於
大於若,則;反之,若,則
基本內容
解釋:當一個數值比另一個數值大時使用大於號">".
其幾何意義可以這樣解釋:
對於任意兩實數a,b,都可在同一數軸上找到其對應點A,B
若點A在點B右側,則a>b
舉例:a=3,b=1,a比b大。即a>b (a大於b)
數學符號
大於號‘>’是數學中不等式運算符號的一種。大於號被廣泛運用在算數中,是國小必學的內容。
英國人哈里奧特於1631年開始採用現今通用之“大於”號“>”及“小於”號“<”,但並未為當時數學界所接受。直至百多年後才漸成標準之套用符號。
龐加萊與波萊爾於1901年引入符號<<(遠小於)和>>(遠大於),很快為數學界所接受,沿用至今。
其他不等式符號
小於號“<”是數學中不等式運算符號的一種。是英國數學家哈利奧特在自己的《使用分析學》( Artis Analyticae Praxis)一書中首先使用了“<”和“>”符號,但是直到他去世十年之後 1631年才發表。a<b,表示a的數值比b的數值小。
大於等於的數學符號為≥。當一個數值比另一個數值大或兩數相等時使用大於等於號"≥",又被稱為“不小於”。對於任意兩實數a,b,都可在同一數軸上找到其對應點A,B。若點A在點B右側或A與B重合,則a≥b。
小於等於是一種判斷方式,用來表示不等式左側的值小於等於不等式右側的值,符號為“≤”。例如3≤5。在各種數學,或編程中會出現。命題中,小於等於是小於或者等於,只要滿足一個條件即可成立。小於等於又稱為不大於。
相關教學
培養學生的符號感,就必須樹立符號意識,有目的、有意識、有計畫、有步驟地滲透於數學教學的始終。在一年級“認數”單元,教材十分注意加強對數的實際意義的理解,在認識了1--5以後,教學幾和第幾的認識,讓學生聯繫生活經驗,體會一個數可以用來表示物體的個數,一也可以用來表示物體排列的/頃序。教材還十分重視幫助學生建立數的大小概念,把握數的大小關係。在教學“=”“>”“<”的認識時,例題提供了童話場景“森林運動會”,從不同動物只數的比較中,抽象出數的大小關係。比較兩種物體數量的多與少,基本方法是一一對應、數形結合。通過一一對應的排列讓學生明確它們的只數,以此建立“同樣多”的概念,在此基礎上用數形結合的方法抽象出“4 =4",認識並理解“=”的含義,使學生知道,當兩個物體個數“同樣多”時,可以用“=”來表示。接著引導學生比較運動會上松鼠和小熊的只數,通過一一對應的排列,使學生明確松鼠只數比小熊多,小熊只數比松鼠少,從而建立“多”“少”的概念,並以此為基礎還用數形結合的方法抽象出“5 >3”和“3 <5",認識理解“>”“<”的含義,學會用“>”“<”表示兩數之間的關係。由此可見,符號意識的培養需要堅實的經驗為基礎,在教學中應促進學生在交流、分享的過程中積累經驗,學習符號化的多種途徑,允許個性化地表示符號;逐步體會用數、形將實際問題“符號化”的優越性,感受符號在理解和解決問題過程中的價值。
例題
在下列()中填寫“=”、“>”、“<”。
a)2()3
b)4*4()5*3
c)10()100-9*9
答案:a)“<”;b)“>”;c)“>”;