詞意介紹
球面上兩點之間的最短距離的航線就是大圓航線。大圓航線是遠距離航行的飛機規劃航路時經常採用的航線。地球是一個橢球體,托球面上的問題解算十分複雜,因此,在實際套用中,往往把地球看做一個正球體。地球面上兩點間最短距離是通過兩點間大圓的劣弧。大圓航線的計算 包括初始航向角、航程、各分點坐標的計算。 大圓航線距離最短,但導航較困難。因此實用中通常採用長距離靠近大圓航線,而短距離走等角航線的作法。
計算公式
地球是一個橢球體,由於橢球扁率的影響,橢球面上的大地問題解算十分複雜。在實際套用中,往往把地球近似看作是一個正球體,這樣,利用球面三角形的相關公式,大圓航線的解算就可以大大地被簡化。
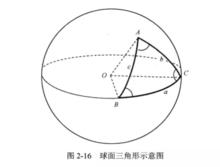
在球面上由三個大圓弧相交於三點所圍成的球面部分稱為球面三角形,構成三角形的大圓弧稱為球面三角形的邊,由兩個大圓弧相交而成的球面角稱為球面三角形的角。AB、AC、BC所圍成的三角形便是一個球面三角形,通常用A、B、C表示球面三角形的三個角;用a、b、c表示球面三角形的三條邊(圖2-16)。這三個角A、B、C和三條邊a、b、c合稱為球面三角形六要素。由於a、b、c都是大圓弧,所以也都可以用弧度表示。
 大圓航線
大圓航線這裡,先介紹三組球面任一三角形的基本公式:
(1)球面正弦公式(2-6):
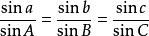 大圓航線
大圓航線(2)邊的餘弦公式(2-7):
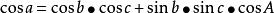 大圓航線
大圓航線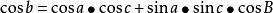 大圓航線
大圓航線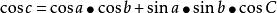 大圓航線
大圓航線(3)球面三角形餘切公式(2-8 四聯公式):
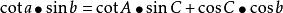 大圓航線
大圓航線 大圓航線
大圓航線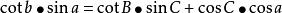 大圓航線
大圓航線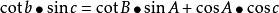 大圓航線
大圓航線 大圓航線
大圓航線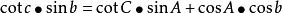 大圓航線
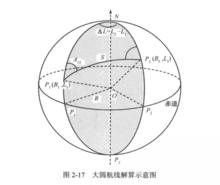
大圓航線這些公式表明了各要素之間的相互計算恭喜,是後面工作的基礎。根據圖2-17,進行解算P、P的大圓航線。
P、P為地球上的兩點,N是北極點。那么P、P,N就構成了一個球面三角形。首先要確定這個三角形的六要素中,哪些是已知的,哪些是要求解的。P的經緯度已知,PN為(90°-B),同理,P的經緯度已知,PN為(90°-B),角N為P、P之間的經緯度差(L-L),這些都是已知的。通過前面列出的公式,不難推出大圓航線距離公式和大圓航線正方位角公式。
 大圓航線
大圓航線大圓航線距離公式為(2-9):
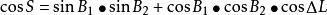 大圓航線
大圓航線大圓航線正方位角公式(2-10):
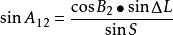 大圓航線
大圓航線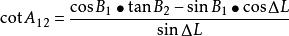 大圓航線
大圓航線用公式計算,S是弧長,單位是弧度(rad),只要乘以地球的平均半徑,就可以得到距離了。初始方位角,用這兩個公式中的任何一個,再用反正弦或反正切,就可以計算出來。但有問題,因為方位角定義為大圓航線與經線的夾角,取值範圍為0°~360°。而反正弦或反餘切的值域都是-90°到90°,不能直接得到0°~360°的航線角,也就是說,我們還必須判斷航線角的象限,然後再進一步處理。這裡得到兩個計算航線角的解算公式,它們恰好可以相互約束,幫我們判斷。
解算思路
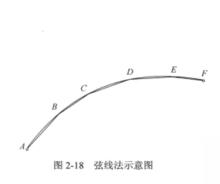
理論上,兩點之間的大圓航線是一條空間曲線,由沿途無數箇中間點組成,所以,在實踐中,我們不可能去解算無數個點的坐標。實際上,我們都是用折線去近似代表這條曲線。所謂的解算,就是去計算有限箇中間點的經緯度坐標。這裡介紹一種稱為弦線法的解算方法。
如圖2-18所示為A、F之間的一條大圓航線,弦線法就是按照一定的經度間隔,計算出航線上相應的中間點B、C、D、E等各點的緯度,然後將這些點連線起來,形成的這條折線就是近似的大圓航線的軌跡。
設P為第i箇中間點,△S為解算的間隔距離(根據精度要求確定),則NPP構成一個球面三角形,其中,已知條件有弧NP、弧PP(即△S)和∠NPP(即A),根據球面三角形的相關公式,即可解出弧NP的值,由此可得到P的緯度(用90°減去弧NP即可)。同時可以解算∠PNP,也就是P和P的經差,進而解算出P的經度,由此,P的經緯度P(B,L)就可以算出來了,就可以得到大圓航線PP之間一系列中間點的經緯度坐標,將這些點連線起來,就可以得到近似的大圓航線軌跡(2-19)。
 大圓航線
大圓航線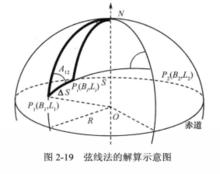 大圓航線
大圓航線