定義
凹多邊形(Concave Polygon)可以有以下三種定義方式:
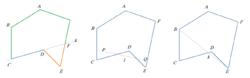 凹多邊形
凹多邊形•至少有一個優角(Reflexive Angle)的多邊形。(例如上圖中,∠CDE>180°)
•把一個各邊不自交的多邊形任意一邊向兩方無限延長成為一直線,如果多邊形的所有邊中只要有一條邊向兩方無限延長成為一直線時,其他各邊不在此直線的同旁(如上圖左),那么這個多邊形就叫做凹多邊形。
•凹多邊形的是一個內部為非凸集的簡單多邊形.簡單多邊形的下列性質與其凸性等價:1、一個內角大於180度。2、存在兩個頂點間的線段位於多邊形的外部。3、多邊形記憶體在兩個點,其連線不全部在多邊形內部。
示例
五角星、 四角星、 八角星、 六角形等都是凹多邊形:例如,正六角星中,有一個240°的角。
性質
•平面上,不可能存在凹三角形。
•凹多邊形的內角和的解,應該通過(n-2)180°來計算。實際上是把大於平角的角劃分為兩個角,使得任意一個凹N多邊形,都可分畫為N-2個三角形,因此凹多邊形的內角和,也適用(N-2)180°這個公式。不可以沿著一條邊的延長線切割凹多邊形。
•平面上,凹多邊形與邊數相同的凸多邊形的內角和相等。
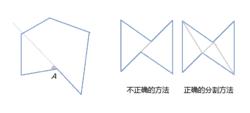 凹多邊形
凹多邊形判斷
對於平面多邊形的三角化處理也是計算機圖形學裡面的一個領域,最近由於項目的需要,需要對平面多邊形進行剖分,特此對其作了些研究。
在對平面多邊形進行處理的時候,很多時候需要知道多邊形的凹凸性,本文介紹兩種方法來進行平面多邊形凹凸性的判定,文章後面會給出示例代碼。
1、使用角度和判斷凹凸性
我們知道,任意n個頂點的凸多邊形可以分解成(n-2)個三角形,一個三角形的內角和是180°,所有三角形的內角和是(n-2)*180°,這一點,對於凸多邊形或者凹多邊形來說都是一樣的,但是對於一個凸多邊形來說,不存在內角大於外角,而凹多邊形則會存在。
因此,將多邊形每個頂點處較小的角(內角或外角)相加,凸多邊形得到(n-2)*180°,而凹多邊形則小於它。至於如何判斷小角,我們可以使用幾何工具---向量點乘。我們知道,向
量點乘可以用來等價求兩個向量的夾角,它的值(即角)總是以較短的弧度來度量的。
以下是代碼的示例:
bool IsHollow(std::vector<Position3> curveloopPoints)const
{
//使用角度和判斷凹凸性:凸多邊形的內角和為(n-2)*180°
auto num = curveloopPoints.size();
float angleSum = 0.0;
for (int i = 0; i < num; i++)
{
Vector3 e1;
if (i==0)
{
e1 = curveloopPoints[num - 1] - curveloopPoints[i];
}
else
{
e1 = curveloopPoints[i - 1] - curveloopPoints[i];
}
Vector3 e2;
if (i==num-1)
{
e2 = curveloopPoints[0] - curveloopPoints[i];
}
else
{
e2 = curveloopPoints[i + 1] - curveloopPoints[i];
}
//標準化並計算點乘
e1.normalize(); e2.normalize();
float mdot = e1%e2;
//計算較小值
float theta = acos(mdot);
//加和
angleSum += theta;
}
//計算內角和
float convexAngleSum = float((num - 2))*YZ_PI;
//判斷凹凸性
if (angleSum<(convexAngleSum-(float(num)*0.00001)))
{/*
if (HollowPoints.size()>0)
{*/
//m_IsHollow = true;
//}
return true;//是凹
}
return false;//否則是凸
}
2、使用矢量判斷凹凸性,檢測多邊形的凸點
檢測多邊形上是否有凹點,如果沒有則為凸多邊形。其原理是,凸多邊形的每個頂點的轉向都應該一致,不一致的點 就是凹點。
我們判斷一個頂點的轉向,使用的是另一個幾何工具---向量叉乘。
這裡我們需要平面的法向量,根據法向量來檢測多邊形的每個頂點:
用相鄰的兩個邊向量計算該頂點的法向量,接著用多邊形的法向量和定點的法向量點乘,若點乘值為負(方向相反),則該頂點就是一個凹點。以下即為示例代碼:
const std::vector<Position3>& IsHollow_Vec(std::vector<Position3> curveloopPoints)const
{
//假設傳進來的頂點數組都是按照順時針或者逆時針遍歷的,且沒有重複點
//使用法向量判斷凹凸性,檢測多邊形上是否有凸點,每個頂點的轉向都應該一致,若不一致則為凹點
std::vector<Position3> HollowPoints;
auto num = curveloopPoints.size();
Vector3 HollowNor = (curveloopPoints[num-1] - curveloopPoints[0])* (curveloopPoints[1] - curveloopPoints[0]);
Vector3 Nor;
for (int i = 0; i < num;i++)
{
if (i==0)//第一個點
{
Nor = (curveloopPoints[0] - curveloopPoints[num - 1])* (curveloopPoints[1] - curveloopPoints[0]);
if ((Nor%HollowNor)>0.0)//如果點乘大於0
{
HollowPoints.push_back(curveloopPoints[i]);
}
}
else if (i==num-1)//最後一個點
{
Nor = (curveloopPoints[i] - curveloopPoints[i - 1])* (curveloopPoints[0] - curveloopPoints[i]);
if (((Nor%HollowNor) > 0.0))//如果點乘大於0
{
HollowPoints.push_back(curveloopPoints[i]);
}
}
else//中間點
{
Nor = (curveloopPoints[i] - curveloopPoints[i - 1])* (curveloopPoints[i+1] - curveloopPoints[i]);
if (((Nor%HollowNor) > 0.0))//如果點乘大於0
{
HollowPoints.push_back(curveloopPoints[i]);
}
}
}
return HollowPoints;
}