外微分形式簡介
微分形式是多變數微積分、微分拓撲和張量分析領域的一個數學概念。現代意義上的微分形式，及其以楔積(wedge product)和外微分結構形成外代數的想法，都是由法國數學家埃里·嘉當引入的。
我們從 R中的開集的情形開始。一個 0-形式（0-form）定義為一個光滑函式 f. 當我們在 R的 m-維子空間 S上對函式 f積分時，我們將積分寫作 ：
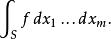外微分形式把 dx, ..., dx當作形式化的對象，而非讓積分看起來像個黎曼和的標記。我們把這些和他們的負− dx, ..., − dx叫做 基本'1 -形式。
我們再在其上定義一種乘法規則楔積，這種乘法只需滿足反交換的條件： 對所有 i, j
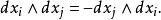外微分形式注意這意味著
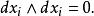外微分形式我們把這些乘積的集合叫做 基本2- 形式，類似的我們定義乘積
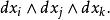外微分形式的集合為 基本'3 -形式，這裡假定n至少為3。定義一個單項式' k-形式為一個0-形式乘以一個基本的 k-形式，定義 k-形式為一些單項式 k-形式的和。
楔積可以推廣到這些和上：
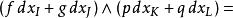外微分形式
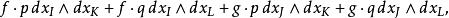外微分形式等等，這裡 dx和類似的項表示 k-形式。換句話說，和的積就是所有可能的積的和。
我們來定義光滑流形上的 k-形式。為此，我們假設有一個開坐標覆蓋。我們可以在每個坐標鄰域上定義一個 k-形式；一個全局的 k-形式就是一組坐標領域上的 k-形式，他們在坐標鄰域的交集上一致。這種 一致的精確定義，見流形。
楔積的性質
若 f, g, w為任意微分形式，則
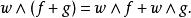外微分形式若 f為 k-形式， g為 l-形式：
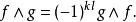外微分形式抽象（簡明）定義及討論
在微分幾何中， k階 微分k-形式是一個流形的餘切叢的 k階外冪（exterior power）的光滑截面。在流形的每一點 p,一個 k-形式給出一個從切空間的 k階笛卡兒冪（cartesian power）到 R的多線性映射。
例如，光滑函式（0-形式）的微分就是一個1-形式。
1-形式在張量的坐標無關表示中是一個很有用的基本概念。在這個上下文中，他們可以定義為向量的的實值函式，並可以看成他們所對應的向量空間的對偶空間。1-形式的一個舊稱就是"協變向量"。
微分形式的積分
k階微分形式可以在 k維鏈（chain）上積分。若 k= 0,這就是函式在點上的取值。其他的 k= 1, 2, 3, ...對應於線積分，曲面積分，體積分等等。
設
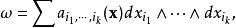外微分形式為一微分形式，設 S為一個我們想在其上積分的集合，其中 S有參數化形式
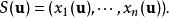外微分形式u屬於參數域 D。則[Rudin, 1976]定義 S上微分形式的積分為
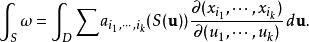外微分形式其中
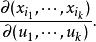外微分形式是雅可比矩陣的行列式 。參見斯托克斯定理（Stokes' Theorem）。
微分形式的操作
一個流形上所有 k-形式的集合是一個向量空間。而且，其上有三類操作：楔積,外微分（用 d表示），和李導數。 d= 0,細節請見德拉姆上同調。
外導數和積分的基本關係由推廣的斯托克斯定理給出，它也同時給出了德拉姆上同調和鏈的同調的對偶性。
