正式定義
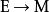向量值微分形式
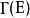向量值微分形式
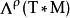向量值微分形式設Μ是一個光滑流形， 是Μ上一個光滑向量場。我們記一個叢Ε截面的空間為 。一個階數為 ρ的 Ε-值微分形式是Ε與 ，Μ的餘切叢的 ρ-次外冪，的張量積叢的一個光滑截面。這樣的形式的空間記作
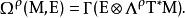向量值微分形式習慣上一個E-值 0-形式就是叢E的一個截面。即
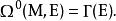向量值微分形式等價地，一個E-值微分形式可以定義為一個完全斜對稱的叢態射
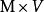向量值微分形式
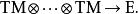向量值微分形式
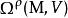向量值微分形式
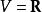向量值微分形式設 V是一個給定的向量空間。一個階數為 ρ的 V-值微分形式是一個取值於平凡叢的微分形式。這樣的形式的空間記作 。當 我們重新得到了通常的微分形式。
向量值形式的運算
拉回
與通常的形式一樣，對向量值形式我們可以定義通過光滑映射的拉回。N上E-值形式通過一個光滑映射 φ:M→N的拉回是M上一個 (φ*E)-值形式，這裡 form onM, where φ*E是E通過 φ 的拉回叢。
公式和通常的情形一樣。對 N上任何一個 E-值 p-形式 ω， 拉回 φ*ω 由
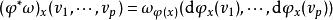向量值微分形式給出。
楔積
與通常微分形式一樣，可以定義向量值形式的楔積。一個E1-值p-形式與一個E2-值q-形式的楔積是一個自然的 (E1⊗E2)-值 (p+q)-形式:
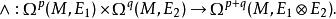向量值微分形式定義就和通常的微分形式一樣，只不過實數乘法為張量積取代：
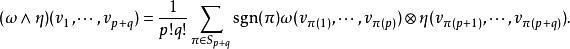向量值微分形式特別地，一個通常（R-值）p-形式與一個E-值q-形式的張量積自然是一個E-值 (p+q)-形式（因為E與平凡叢M×R的張量積自然同構於E）。對ω∈ Ω(M) 和η∈ Ω(M,E) 我們有通常的交換關係：
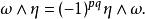向量值微分形式一般地，兩個E-值形式的楔積不是另一個E-值形式，而是一個 (E⊗E)-值形式。但是，如果E是一個代數叢（也就是一個代數的叢而不僅僅是向量空間）則與E中的乘法複合得到一個E-值形式。如果E是一個交換結合代數，則在此修改後的楔積下，所有E-值微分形式的集合
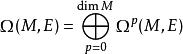向量值微分形式成為一個分次交換結合代數。如果E的纖維不交換則 Ω(M,E) 不是分次交換的。
外導數
對任何向量空間V，V-值微分形式上有一個自然的外導數。這只不過是通常的外導數作用在關於V的任何一個基的分量上。具體地說，如果 {eα} 是V的一個基，則V-值p-形式 ω = ωeα的微分為：
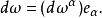向量值微分形式更一般地，上面的注可套用於M上任何平坦向量叢（即一個轉移函式是常數的向量叢）E之E-值形式。上面定義的外微分是E的任何局部平凡化。
如果E不是平坦的則E-值形式上沒有自然的外微分。需要在E上選取一個聯絡。E上一個聯絡是一個將E的界面變為E-形式的線性微分運算元：
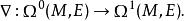向量值微分形式如果E裝備有一個聯絡 ∇，則有惟一的一個共變外微分延拓了 ∇
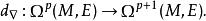向量值微分形式共變外微分由線性與等式
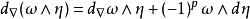向量值微分形式刻畫，這裡 ω 是一個E-值p-形式而η 是一個通常的q-形式。一般地，不一定有d∇= 0。事實上，這若且唯若聯絡 ∇ 平坦（即曲率消失）。
李代數值形式
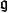向量值微分形式 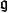向量值微分形式向量值形式一個重要的特例是李代數值形式。設 是一個李代數，則有 -值形式。這樣的形式在主叢的聯絡以及嘉當聯絡的理論中有重要套用。
因為任何李代數有一個雙線性李括弧運算，兩個李代數值形式的楔積可與李括弧運算複合得到另一個李代數值形式。這個運算通常記為 [ω∧η]，表明涉及兩個運算。例如如果 ω 和 η 是李代數值1-形式，則有
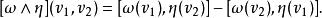向量值微分形式在此運算下一個流形M上所有李代數值形式成為一個分次李超代數。
主叢上的基本或張量性形式
設E→M是M上一個秩k光滑向量叢，π: F(E) →M是E（相伴的）標架叢。E通過π的拉回同構於平凡叢 F(E) ×R。從而，M上一個E-值形式的拉回決定了 F(E) 上一個R-值形式。不難檢驗這個拉回形式關於 GLk(R) 在 F(E) ×R上的自然作用左等變，且在鉛直向量取值上為零（F(E) 位於核 dπ中的切向量）。F(E) 上這樣的向量值形式之重要足以獲得一個特別的名字：他們被稱為 F(E) 上的基本或張量性形式。
設π:P→M是一個（光滑）主G-叢，令V是一個固定的向量空間以及表示ρ:G→ GL(V)。P上一個 ρ 型基本或張量性形式是水平且等變的，如果：
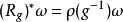向量值微分形式1. 對所有g∈G，且
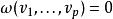向量值微分形式2. 其中至少有一個vi是鉛直的（即 dπ(vi) = 0）。
這裡Rg表示通過g∈G的左平移。注意這對 0-形式第二個條件是空虛的真（vacuously true）。
給定P和ρ如上，我們定義構造相伴叢E=P×ρV。P上的張量性形式一一對應於M上的E-值形式。與主叢 F(E) 的情形一樣，M上E-值形式拉回到P上的V-值形式，這正好是P上的 ρ 型基本或張量性形式。反之給定P上任何一個 ρ 型張量性形式我們直接地可以構造M上的相應的E-值形式。
