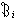堅韌檢測

堅韌檢測是現代檢測理論的一個分支。用經典參量檢測理論解決從噪聲中提取信號問題，往往會遇到對背景噪聲的統計特性缺乏先驗知識的困難。

堅韌檢測

正文

現代檢測理論的一個分支。用經典參量檢測理論解決從噪聲中提取信號問題，往往會遇到對背景噪聲的統計特性缺乏先驗知識的困難。堅韌檢測是為了克服這一困難而發展起來的。與參量檢測方法比較，堅韌檢測的特點是不需要確定的噪聲機率分布模型，而是以首先假設與實際噪聲相近似的一族分布函式作為解決問題的起點。曾經提出過幾種分布函式族模型，對於下式的混合模型的研究最為廣泛：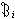

＝｛F＝(1－ε)Gi+εHi,Hi∈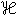｝(0＜ε＜1；i＝0.1)

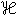式中Gi為一個確定的分布函式；ε稱為污染度； 為一類很寬的分布函式集；F為集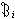的元素。F中的第一項是對噪聲統計特性確知部分的描述,第二項是對噪聲統計特性中不確定性的描述,ε則表示不確定性的權重。當ε較小時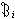，中的任一元素F均很接近名義分布函式Gi;當ε較大時，分布就變得複雜。從上式所列模型出發，根據實際問題中給定的準則，在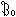和中尋找一對最不利分布，在數學上就是要求出一個下確界。然後，從這對最不利分布出發，用參量檢測理論中的統計判決方法求出一個上確界，構造出最佳檢測器，這樣就使檢測理論能適應較複雜的背景噪聲，具有工程實用意義。

配圖

相關連線