動力學系統函式尋優

在一組約束條件下,尋找動力學系統的一組函式,直接函式尋優法是計算機仿真中常用的方法。

動力學系統函式尋優

正文

在一組約束條件下,尋找動力學系統的一組函式,使給定的指標達到最優值（極小或極大值）的方法，屬於多次運行仿真。動力學系統函式尋優方法有三類：極大值原理法（見極大值原理）、動態規劃法(見動態規劃)和直接函式尋優法。前兩種方法只能處理最優控制問題，即被尋優的函式是以時間為自變數的。
直接函式尋優法是計算機仿真中常用的方法。它的基本思路是先將被尋優的函式表示成一些已知的基函式的代數和，從而將對函式的尋優轉變成為對這些代數項的權係數尋優，即變成為參數尋優問題。以一個尋優函式u(x)為例，設u(x)能表示成：

其中lj(x)是定義在【ɑ，b】上的已知標量基函式,αj是可調權係數(參數)。給出一組參數α1，α2，…，αm，便確定一個函式 u(x)。x可以是系統中的狀態變數或時間變數。基函式lj(x)可以是階梯形函式、折線形函式、多點插值函式等。當選定基函式後，函式u(x)的尋優問題便轉變成一組參數(α1,α2,…,αm)的尋優問題。如果在系統模型中加入實現上式的函式插值器，則函式的疊代尋優過程與參數尋優類同（見動力學系統參數尋優）。
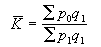
對於n個函式尋優的情形，有n個相應的上述表達式，也就有n×m個參數尋優。

配圖

相關連線