埃爾米特函式

埃爾米特函式(Hermitian function)一種特殊的半雙線性函式。 在數學分析的領域中，埃爾米特函式是當一個函式的共軛複數與將原函式的自變數變號後的值相等的複變函數。

定義

在數學分析的領域中， 埃爾米特函式是當一個函式的共軛複數與將原函式的自變數變號後的值相等的複變函數。對於所有在f定義域內的所有x 滿足:

埃爾米特函式

（其中上橫線表示復共軛）

埃爾米特函式

這個定義也可以擴展到兩個或多個變數的函式，例如，對於兩個變數的函式 f，當 f 定義域內的所有數對 滿足

埃爾米特函式

時，它為埃爾米特函式。

根據這個定義,可得出一個很顯然的推論:若且唯若

f 的實部為偶函式，並且

f 的虛部為奇函式

時，f 是埃爾米特函式。

套用

埃爾米特函式經常出現在數學、物理和信號處理中。根據傅立葉變換的基本性質，可以得出以下兩條敘述：

•實函式的傅立葉變換為埃爾米特函式

•埃爾米特函式的傅立葉變換為實函式

由於實信號的傅立葉變換可以保證是埃爾米特函式，因而可以將埃爾米特奇/偶對稱性用於壓縮。這使得經過離散傅立葉變換的信號（為一般複數）可以存儲在與原實數信號相同的空間中。

埃爾米特函式

若 f為埃爾米特函式，則

埃爾米特函式

埃爾米特函式

其中是互相關，而 是卷積。

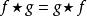埃爾米特函式

若 f與 g都是埃爾米特函式，則。