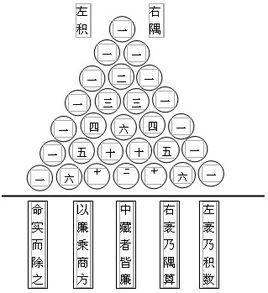
垛積問題
朱世傑在《四元玉鑒》中記載了許多高階等差數列的問題，他列下了一串美麗的級數求和公式：
菱草垛
（等差數列）
1+2+3+……+n=n（n+1）/2!
即Σr= n（n+1）/2!
三角垛
垛積等差數列表（二階等差數列）
1+3+6+……+ n（n+1）/2= n（n+1）（n+2）/3!
即Σr（r+1）/2! = n（n+1）（n+2）/3!
撤星形垛
（三階等差數列）
1+4+10+……+ n（n+1）（n+2）/3!= n（n+1）（n+2）（n+3）/4!
即Σr（r+1）（r+2）/3! =n（n+1）（n+2）（n+3）/4!
三角撤星形垛
（四階等差數列）
1+5+…+ n（n+1）（n+2）（n+3）/4!= n（n+1）（n+2）（n+3）（n+4）/5!
即Σr（r+1）（r+2） （r+3）/4! =n（n+1）（n+2）（n+3） （n+4）/5!
更落一形垛
（五階等差數列）
1+6+21+……+ n（n+1）（n+2）（n+3）（n+4）/5!
=Σr（r+1）（r+2） （r+3）（r+4）/5!
= n（n+1）（n+2）（n+3）（n+4）（n+5）/6!
定義及公式
我們可以看出他的三角垛公式是以草垛的和為一般項，而撤星形垛是以三角形垛的和為一般項，並且連績以新級數的和為一般項，求出另一新的高階等差級數的公式。從他用「落一形垛」、「更落一形垛」的名稱，可以知道，他是將前式的r項和是後式的第r項，即前式中到第r層為止的垛積降落一層是後式垛積的第r層。
從以上的一串公式，朱世傑歸納得一般式：
Σr（r+1）（r+2）……（r+p-1）/p!=n（n+1）（n+2） ……（n+p-1）/（p+1）!
李善蘭的研究
李善蘭介紹
李善蘭像李善蘭（1811—1882），字壬叔，號秋紉，浙江省海寧人。
自幼喜愛數學，1845年，撰《方園闡幽》、《弧矢啟秘》、《對數探源》，在三角函式、對數函式的冪級數展開式的研究上取得比前人更大的成就，他創造的尖錐術提出了幾個定積分公式，在接觸西方微積分之前，獨立地跨進了微積分的門檻。
1852年，離開家鄉到上海，與英國傳教士偉烈亞力合譯《幾何原本》後9卷，《代數術》13卷，《代微積拾級》18卷，後者是中國第一部微積分學譯著。
李善蘭《垛積比類》書影同時，李善蘭會通中西，寫出《橢圓正術解》等四種關於圓錐曲線的研究著作，《級數回求》等關於冪級數的研究著作。
垛積問題研究
《垛積比類》書影《垛積比類》是中國特色的垛積問題研究專著，為關於高階等差級數求和的著作。
李善蘭恆等式為組合數學中的一個恆等式，由中國清代著名數學家李善蘭先生於1859年在《垛積比類》一書中首次提出，因此得名。
