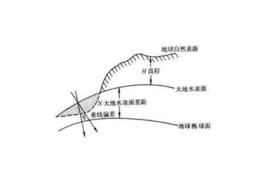
定義
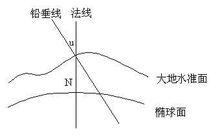 垂線偏差
垂線偏差同一測站點上鉛垂線與橢球面法線之間的夾角u,即是 垂線偏差。
u通常用南北方向分量ζ和東西方向分量η表示。參見右圖。
垂線偏差的另一定義是地麵點的垂線方向同正常重力方向之間的夾角。這兩種定義的差異,就是正常重力方向同橢球面法線之間的夾角,它位於子午面內。這個差值可以從理論上算出。兩種垂線偏差可以相互換算。
垂線偏差可以用於計算高程異常、大地水準面差距,推求平均地球橢球或參考橢球的大小、形狀和定位,並用於天文大地測量觀測數據的歸算,也用於空間技術和精密工程測量。按選取的橢球不同,垂線偏差可分為絕對垂線偏差和相對垂線偏差。
垂線偏差分類
絕對垂線偏差
又稱重力垂線偏差,是垂線同平均地球橢球面法線之間的夾角。因為平均地球橢球是不變的,所以過地麵點的法線或正常重力線也是不變的。因而垂線偏差具有絕對意義,它可以利用重力異常,按韋寧·邁內茲公式計算。
在經典的地球形狀理論中,需要知道大地水準面上的垂線偏差,因而需將地麵點的垂線歸算到大地水準面上,組成大地水準面上相應的垂線偏差。由於這種歸算同大地水準面和地面間的質量分布有關,而尚不能準確地知道這種分布,因此,計算大地水準面上的垂線偏差分量,理論上就不可能是嚴密的。為了避免這種不嚴密性,可採用莫洛堅斯基理論計算地麵點的垂線偏差。用零次趨近的莫洛堅斯基公式計算的地面垂線偏差和用韋寧·邁內茲公式算出的數值是一樣的。
在重力資料稀少的情況下,垂線偏差還可以根據地殼均衡假說來計算,這樣的垂線偏差稱為地形均衡垂線偏差。
相對垂線偏差
又稱天文大地垂線偏差,是垂線和參考橢球面的法線之間的夾角。因為不同的參考橢球過地麵點的法線不同,垂線偏差也各不相同,所以它具有相對意義。相對垂線偏差可以利用天文和大地經緯度來計算。
計算公式
(1)垂線偏差公式:
ξ=φ-B,η=(λ-L)cosφ。已知一點的天文和大地經、緯度,就可求得垂線偏差。
(2)拉普拉斯方程:
A=α-(λ-L)sinφ-(ξsinA-ηcosA)cotZ(天)
簡化 A=α-(λ-L)sinφ 或 A=α-ηtanφ
(3)這樣可以將天文方位角α歸算為大地方位角A。
天文緯度φ、經度λ同大地緯度B、經度L的關係:B= φ-ξ;L= λ-ηsecφ
依據上式,便可將天文緯度和經度換算為大地緯度和經度。
衛星測高中的垂線偏差法
研究背景
當前國際上利用衛星測高數據反演海洋重力場的方法主要有5 種:①最小二乘配置法;②Stokes公式逆運算法;③Hotine 公式逆運算法;④直接求解法;⑤垂線偏差方法等。其中,最小二乘配置法需要預先確定各參量之間的協方差陣並解算大型矩陣,Stokes、Hotine 公式的逆運算法易受動力海面地形模型誤差的影響。而直接求解法在理論上存在一些近似。由於海面高的一次差分技術可以有效減弱動力海面地形、測高衛星徑向軌道誤差等長波誤差的影響,精確計算大地水準面在經、緯度方向的梯度,從而精確確定海域大地水準面上的測高垂線偏差;另一方面,根據物理大地測量的邊值理論,各擾動場元之間存在固定的函式關係。因此,可以利用大地水面上高精度的測高垂線偏差計算海洋上高精度的大地水準面、重力異常等擾動場元,上述理論即為衛星測高中的“垂線偏差法”。它為利用衛星測高資料反演高精度、高解析度的海洋重力場提供了理論依據,標誌著衛星測高技術在大地測量中的套用逐步趨於成熟。
垂線偏差法需要先利用衛星測高數據計算海洋上的測高垂線偏差,Sandwell、Olgiati、Hwang先後提出了不同的測高垂線偏差計算方法,它們也是當前國際上測高垂線偏差的主要計算方法。垂線偏差法的另一重要步驟是如何利用測高垂線偏差精確計算海洋重力場,Molodenskii、Sandwell、Hwang 等在不同時期分別提出了各自利用垂線偏差法確定海洋重力場的原理,尤其是Molodenskii、 Hwang利用測高垂線偏差計算海域大地水準面和重力異常的方法在理論上比較嚴密,在實際工程中套用得比較普遍。研究將重點研究Sandwell 、Olgiati 、 Hwang 三種測高垂線偏差的計算方法和 Molodenskii、 Hwang利用測高垂線偏差法確定海洋大地水準面和重力異常的原理,分析比較了它們之間的異同,總結了它們的優缺點,為科學地利用衛星測高數據反演海洋重力場提供理論依據。
測高垂線偏差的計算方法
計算測高剖面垂線偏差的基本原理就是根據測高點測高記錄中的位置和時間信息,利用測高數據的一次差分計算測高剖面的數據導數,進而計算海洋上的測高垂線偏差。
測高垂線偏差計算方法間的比較
據上文可知,Sandwell 垂線偏差計算方法僅能計算海洋上測高衛星地面軌跡交叉點的(ξ, η ),利用該方法計算了TOPEX/POSEIDON、ERS -1/2在單個覆蓋周期內的交叉點及該點的(ξ, η )。鑒於測高衛星的“凍結”軌道特徵,測高衛星在各覆蓋周期內地面軌跡交叉點的位置精確重複,但由於不同周期不同觀測環境的影響,各周期測高衛星地面軌跡在海洋上的有效交叉點數目不盡相同。實驗計算結果表明,TOPEX/POSEIDON 衛星地面軌跡交叉點每周期有 7000 個左右,ERS -1/2 衛星(在覆蓋周期為 35 天時)約為55000,其空間分布比較稀鬆,也不均勻。因此,Sandwell 測高垂線偏差計算方法雖然理論嚴密,在交叉點計算的垂線偏差的精度也比較高,但不能滿足利用衛星測高資料反演高解析度海洋重力場的要求 。
Olgiati 測高垂線偏差計算方法能夠計算測高衛星沿跡逐個採樣觀測點和交叉點的(ξ, η ),(ξ, η ) 的空間解析度很高,為利用衛星測高數據反演高解析度海洋重力場提供了條件。但該方法需沿軌跡於相鄰交叉點之間各觀測點處內插在垂直於軌跡方向的垂線偏差,影響了(ξ, η )的精度和最終所反演重力場的質量。
由於上述兩種方法得到的(ξ, η )不規則地分布在觀測點或交叉點上,在利用它們計算海洋重力場之前,還必須將其處理成均勻格網上的平均值(ξ, η )。而 Hwang 先利用測高數據計算各觀測點在沿跡方向的垂線偏差 ε,然後根據觀測方程(10)直接計算測高垂線偏差子午、卯酉分量在格網上的平均值( ξ, η )。該方法不僅理論嚴密,而且
不需要計算測高衛星地面軌跡的交叉點,計算過程簡便,所得(ξ, η )的解析度比較高,如利用Seasat、Geosat、TOPEX/POSEIDON 衛星測高資料可計算全球 82° S ~ 82° N 海域 2′×2′ 的(ξ, η ),使利用衛星測高資料反演高精度、高解析度海洋重力場成為可能。