幾何定向特點
定向精度：與起始方位精度和觀測儀器等級有關。
實時性：需觀測傳遞方位的多個轉折角，無法做到實時性。
自主性：完全自主。
受外界影響：受外界條件影響很多，如大風會影響儀器的穩定，地而輻射熱會影響大氣的穩定，大氣透明度會影響照準精度，溫度變化會影響儀器的正常狀態等。
成本：成本低。
功能：獲取坐標方位 。
一井定向
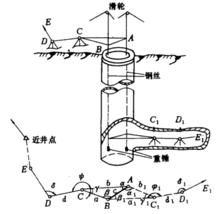圖1 一井定向在一個立井中自由懸掛兩根鋼絲垂線，由地面向井下傳遞平面坐標和方向的測量工作。如圖，在井筒中自由懸掛兩根鋼絲垂線A、B，它代表一個鉛垂面，利用該面上的任一條直線都具有相同的方位角和垂線上任一點的平面坐標都相同的原理，將地面平面坐標和方向傳遞到井下。一井定向工作，除定向投點和井上、下連線測量外，還需進行地面連測導線測量，以求得地面連線測量的起算數據 。
地面連測導線測量
地面由近井點至連線點的導線稱為地面連測導線。定向之前，必須在地面井口附近設立作為定向時與鋼絲垂線連線的點C(井下為C)，稱為連線點。由近井點開始測設地面連測導線，以求出連線點C的坐標及連線邊CD的坐標方位角，作為地面連線測量的起算數據。中國《煤礦測量規程》規定的精度要求為：測角中誤差不超過±5″，導線全長相對閉合差不超過1/10000。對小煤礦，可適當放寬要求 。
定向投點
定向投點可用鋼絲投點或雷射鉛垂儀投點。中國廣泛採用鋼絲投點。用鋼絲投點時，鋼絲上端固定在地面，下端(在定向水平上)懸掛重錘(垂球)，並將重錘放入水桶中，以減少鋼絲垂線的擺動。
鋼絲投點方法分為單重投點和多重投點。
單重投點法，是在投點的過程中，垂球的重量保持不變。多重投點法則是在投點的過程中，利用改變垂球的重量來確定地面鋼絲垂線點在定向水平上的正確位置。單重投點法較之多重投點法作業簡單，效率高，得到廣泛套用。單重投點法又分為單重穩定投點和單重擺動投點兩種。前一種是將垂球(重錘)放在水桶中，使其靜止，在定向水平上就與靜止的鋼絲垂線進行連線測量。後一種是用經緯儀觀測垂線的自由擺動以確定其穩定位置，並加以固定，在定向水平上就與此固定的鋼絲垂線進行連線測量。垂線的擺幅很小能基本靜止時，採用穩定投點，否則須採用擺動投點 。
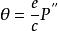幾何定向由於井筒內氣流、滴水等的影響，鋼絲垂線在地面的位置投到定向水平後會發生偏離，這種線量偏差稱為投點誤差。由投點誤差引起的兩垂線連線的方向誤差，叫做投向誤差。投向誤差 θ 按下式計算：，式中 e 為鋼絲投點誤差，m；c 為兩垂線間的距離，m；ρ″=206265″ 為每弧度的角秒數。
兩垂線間的距離 c 受井筒直徑的限制，一般為4m左右，因而由投點誤差引起的投向誤差是很大的，成為一井定向誤差的主要來源。為此，減少投點誤差的措施為：定向時停止風機運轉或增設風門，以減少風速；在井下採用防風套筒套著垂線，以隔離風流對鋼絲的作用；採用直徑小、抗拉強度高的鋼絲，適當加大重錘的重量，並將重錘放入穩定液中。此外，應儘量增大兩垂線間的距離，以減少投向誤差 。
連線測量
連線測量工作可採用三角形連線法、瞄直法和四邊形法。
三角形連線法：以連線點和井筒中兩垂線構成延伸三角形(圖1的ΔABC和ΔABC)進行一井定向的連線測量方法，是一種套用廣泛的地面與井下連線測量方法。
(1)三角形圖形要求。從連線測量誤差儘量小的觀點出發，c邊愈長，a/c(或a1/c)、γ(或γ)角愈小的延伸三角形是最有利的連線圖形。
(2)施測。地面連線測量時，在C點測量水平角γ、φ；用鋼尺精確丈量a、b、c三邊長。井下連線測量時，同法測量γ、φ角度和三角形三邊長度。此外，井上下還須分別測量δ、δ角及d、d邊長。
(3)計算。地面和井下垂線處不能直接測量的角度α、β和α、β
(4)定向誤差估算。為設計定向工作，需對定向誤差進行估算。
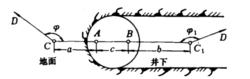圖2 瞄直法瞄直法：又名穿線法。如圖2，用瞄線法將地面連線點C與井下連線點C分別設定在兩垂線A、B的延長線上，即C-A-B-C位於同一豎直平面內。在C與C點安置經緯儀測出角度φ、φ，量出CA、AB和BC的長度，就能按導線D-C-C-D計算出井下C點的坐標和CD邊的坐標方位角 。
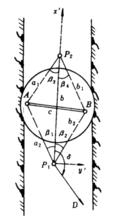圖3 四邊形連線法四邊形連線法：井下連線測量的一種方法。當受井口、井筒和井底車場的條件限制，必須在與兩垂線連線的大致垂直方向連線時，採用此法。如圖3，井下連線點P、P與兩垂線A、B構成四邊形。根據兩已知點A、B來確定兩未知點P、P的平面坐標及其連線的坐標方位角 。
兩井定向
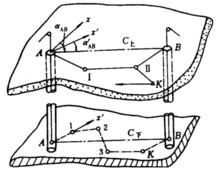圖4 兩井定向在有井下巷道相連通的兩個立井中各掛一根鋼絲垂線由地面向井下傳遞平面坐標和方向的測量工作。如圖4，在兩個立井中各掛一根鋼絲垂線A、B，由地面控制點K敷設導線測定兩垂線的坐標，在井下兩垂線間敷設經緯儀導線，經計算將地面平面坐標及方向傳遞到井下。兩井定向工作包括定向投點，井上、下連線測量及其計算。
地面連線測量
地面連線測量的目的在於測定兩鋼絲垂線的坐標。由近井點K向兩垂線A、B測設連線導線K-Ⅱ-Ⅰ-A及K-Ⅱ-B，算出兩垂線的坐標x、y及x、y
井下連線測量
在井下定向水平，沿兩井間相通的巷道測設井下經緯儀導線A-1-2-3-4-B。以垂線A的地面坐標為起算數據，根據井下導線各邊的坐標方位角和邊長計算井下導線各點的坐標，完成定向任務。
測量和計算的檢查
用比較井上與井下算得的兩垂線間距離c和c進行檢查。
兩井定向與一井定向相比，投點誤差對定向精度的影響大大減小，連線測量作業簡單，占用井筒時間少，定向精度高 。
經緯儀進行幾何定向簡介
在傳統測量中，無論是測角網、測邊網、邊角網，還是附合導線、閉合導線和支導線的布設，通過角度測量傳遞已知方位是確定地麵點位的基本測量工作之一，常用的角度測量儀器有經緯儀、全站儀。由於單從角度測量而言，經緯儀與全站儀等價，故此以經緯儀為例敘述 。
要通過經緯儀實現定向功能，確定出地面任意兩點連線的坐標方位，必須具備已知起始數據：一已知坐標方位或兩已知坐標，故該定向法誤差包含有已知起始方位誤差，其次是水平角觀測誤差。在水平角觀測誤差中有各種各樣的誤差來源，其中誤差來源不同對水平角觀測的精度也有著不同的影響，主要包括五方面的誤差來源：1)儀器誤差；2)儀器對中誤差；3)目標偏心誤差；4)照準誤差與讀數誤差；5)外界條件的影響。其中儀器誤差有屬於製造方面的，如水平度盤偏心與刻劃誤差、水平度盤與豎軸不垂直等；有屬於校正不完善的，如豎軸與照準部水準管軸不完全垂直，視準軸與橫軸的殘餘誤差。至於儀器對中誤差和目標偏心誤差均屬於“對中”性質的誤差，就對中本身而言是偶然誤差，可是一旦目標標誌和儀器已經安置，則對中誤差的真值不再發生變化，因此該誤差在一次架站中又具有系統性。另外，讀數誤差主要是針對光學經緯儀而言的，取決於儀器的讀數設備，而電子數顯經緯儀則不存在該誤差 。
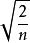幾何定向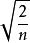
幾何定向 幾何定向對於水平角觀測精度，通常以某級經緯儀的標稱精度作為基礎，套用誤差傳播定律進行分析。設某級經緯儀室外一測回方向中誤差為m，則一測回角值中誤差為m，如按 n 測回觀測水平角，則m=m。故幾何定向法的精度可表示為：m=m+m 。
