簡介
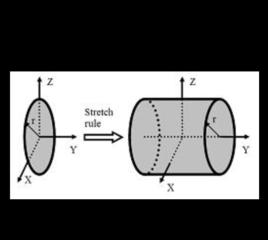
在物理學裡， 伸展定則闡明，如果將一個物體的任何一點，平行地沿著一支直軸作任意大小的位移，則此物體對此軸的轉動慣量不變。
我們可以想像，將一個物體，平行於直軸地，往兩端拉開。在物體伸展的同時，保持物體任何一點離直軸的垂直距離不變，則伸展定則闡明此物體對此軸的轉動慣量 不變。
伸展定則、垂直軸定理、平行軸定理，這些工具都可以用來求得許多不同形狀的物體的轉動慣量。
相關定理
垂直軸定理
在物理學裡， 垂直軸定理（也叫“正交軸定理”）可以用來計算一片薄片的轉動慣量。思考一個直角座標系，其中兩個座標軸都包含與平行於此薄片；如果已知此薄片對於這兩個座標軸的轉動慣量，則垂直軸定則可以用來計算薄片對於第三個座標軸的轉動慣量。
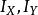伸展定則假設OXYZ座標系統的 X-軸與 Y-軸都包含與平行於此薄片，而 Z-軸垂直於薄片的面。分別代表薄片對於 X-軸與 Y-軸的轉動慣量．那么，薄片對於 Z-軸的轉動慣量為
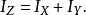伸展定則平行軸定理
平行軸定理（英語： parallel axis theorem）能夠很簡易地，從剛體對於一支通過質心的直軸（質心軸）的轉動慣量，計算出剛體對平行於質心軸的另外一支直軸的轉動慣量。
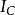伸展定則讓代表剛體對於質心軸的轉動慣量、M代表剛體的質量、d代表另外一支直軸 z'-軸與質心軸的垂直距離。那么，對於 z'-軸的轉動慣量是
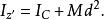伸展定則轉動慣量
在古典力學中， 轉動慣量又稱 慣性矩，通常以 表示，國際單位制基本單位為[kg]·[m2]。轉動慣量用以描述一個物體對於其旋轉運動的改變的對抗，是一個物體對於其旋轉運動的慣性。轉動慣量在旋轉動力學中的角色相當於線性動力學中的質量，描述角動量、角速度、力矩和角加速度等數個量之間的關係。
實例
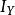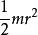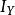伸展定則
伸展定則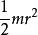 伸展定則 伸展定則圓板對於 Y-軸的轉動慣量是 。將圓板沿 Y-軸伸展成實心圓柱，其對於 Y-軸的轉動慣量仍舊是。
