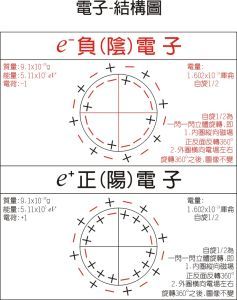
簡介
在固體物理學中, 緊束縛近似是將在一個原子附近的電子看作受該原子勢場的作用為主,其他原子勢場的作用看作微擾,從而可以得到電子的原子能級和晶體中能帶之間的相互關係的一種近似計算手段。在此近似中,由於我們假定能帶是由各個孤立原子的波函式疊加而來的,因此能帶的電子波函式可以寫成布洛赫波函式之和的形式:
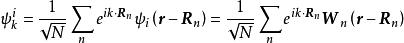 緊束縛近似
緊束縛近似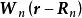 緊束縛近似
緊束縛近似其中 被稱為瓦尼爾函式。此近似和化學中的原子軌道線性組合(Linear combination of atomic orbitals, LCAO)的關係緊密。和近自由電子近似不同,緊束縛模型適用範圍大得多。
瓦尼爾函式
瓦尼爾函式( Wannier function,或 沃尼埃函式),是固體物理學中的一個正交函式的完備集,由格里高利·瓦尼爾提出。瓦尼爾函式在晶系中對應著局域化分子軌道。
晶體中不同晶位的瓦尼爾函式所具有的正交性,使得對特定區域中的電子態進行展開時可以構造出便於計算的基組。瓦尼爾函式的套用極其廣泛,例如對電子結合能的分析,在對激子以及里德伯物質的分析中也有其特定的套用。
原子軌域線性組合
原子軌域線性組合(Linear combination of atomic orbitals,或者簡寫為LCAO),是量子化學中用於求解分子軌域的一種方法,這種方法是通過對原子軌域進行線性疊加來構造分子軌域。因為它屬於分子軌域方法的一種,所以又稱原子軌域線性組合的分子軌域方法,或者叫LCAO-MO。它於1929年由Sir John Lennard-Jones引入用於描述元素周期表第一行上原子構成的雙原子分子的成鍵,並且經由Ugo Fano進行了擴展。
在量子力學裡,原子的電子排布由波函式來描述。從數學上來看,這些波函式構成了函式基組。在化學反應過程中,軌道波函式會發生改變,根據原子所參與形成的化學鍵的類型,電子云的形狀會相應改變。
參見
•軌道磁化
•布洛赫波
•Hannay角