定義
 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式嚴格凹函式是定義在某個向量空間的凸子集C(區間)上的實值函式 (x) ,而且對於凸子集C中任意兩個向量p,q, 滿足
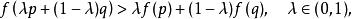 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式則稱 是定義在凸子集C中的嚴格凹函式。容易證明,其定義等價於若 滿足
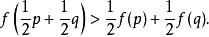 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式對任意兩個向量p,q成立。特別地,若這裡凸集C即某個區間 I ,那么就是:設 為定義在區間 I 上的函式,若對 I 上的任意兩點 和 ,有
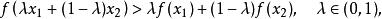 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式成立,則稱 是定義在區間I 中的嚴格凹函式。
在上面的定義中,若將小於號改變小於等於,則上面的函式稱之為凹函式。
判別方法
引理
 嚴格凹函式
嚴格凹函式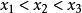 嚴格凹函式
嚴格凹函式為 I上的凹函式的充要條件是:對於I的任意三點 ,總有
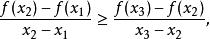 嚴格凹函式
嚴格凹函式證明:
必要性:
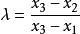 嚴格凹函式
嚴格凹函式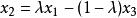 嚴格凹函式
嚴格凹函式設 ,則有 ,由凸性的定義代入,從而有
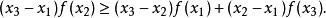 嚴格凹函式
嚴格凹函式整理後即可得到。
充分性:
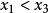 嚴格凹函式
嚴格凹函式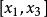 嚴格凹函式
嚴格凹函式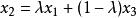 嚴格凹函式
嚴格凹函式在I上任取兩點 ,在 上任取一點 ,由必要性的推導逆過程,可證得
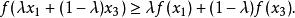 嚴格凹函式
嚴格凹函式故為I上的凹函式。 證畢。
推論1
 嚴格凹函式
嚴格凹函式為 I上的函式,下列條件等價:
 嚴格凹函式
嚴格凹函式1) 為 I上的凹函式的。
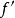 嚴格凹函式
嚴格凹函式2)為I上的減函式。
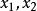 嚴格凹函式
嚴格凹函式3) 對I上的任意兩點 ,有
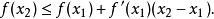 嚴格凹函式
嚴格凹函式推論2
對於實數集上的函式,如果其二階導數在區間上非正,就為凹函式。如果其二階導數在區間上恆小於0,就為嚴格凹函式 。
嚴格凹函式的性質
1)一元可微函式在某個區間上是嚴格凹的,若且唯若它的導數在該區間上嚴格單調減的。
 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式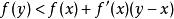 嚴格凹函式
嚴格凹函式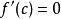 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式2)一元連續可微函式在區間上是嚴格凹的,若且唯若函式位於所有它的切線的下方:對於區間內的所有和,都有 。特別地,如果 ,那么c是 的最大值。
3)一元二階可微的函式在區間上是嚴格凹的,若且唯若它的二階導數是負的;這可以用來判斷某個函式是不是嚴格凹函式,但反過來不成立。更一般地,多元二次可微的連續函式在凸集上是嚴格凹的,若且唯若它的黑塞矩陣在凸集的內部是嚴格負定的。
4)嚴格凹函式的任何極大值也是最大值。嚴格凹函式最多有一個最大值。
 嚴格凹函式
嚴格凹函式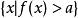 嚴格凹函式
嚴格凹函式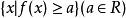 嚴格凹函式
嚴格凹函式5)對於嚴格凹函式 ,水平子集 和 是嚴格凸集。
 嚴格凹函式
嚴格凹函式6)反向延森不等式 對嚴格凹函式 都成立。
 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式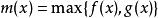 嚴格凹函式
嚴格凹函式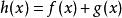 嚴格凹函式
嚴格凹函式7)如果和是嚴格凹函式,那么和也是嚴格凹函式。
 嚴格凹函式
嚴格凹函式 嚴格凹函式
嚴格凹函式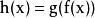 嚴格凹函式
嚴格凹函式8)如果和是嚴格凹函式,且g遞減,那么是嚴格凹函式。
 嚴格凹函式
嚴格凹函式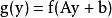 嚴格凹函式
嚴格凹函式9) 凸性在仿射映射下不變:也就是說,如果是凹函式,那么也是凹函式。
等等性質。
注
某些教材的凹函式定義與此定義相反,即凸函式與凹函式相反。如北京大學版本和中山大學的數學教材。
