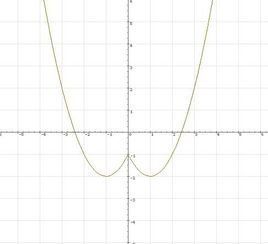
定義
一個有實值函式f在某區間中(或者在某個向量空間中的凹集),任意x和y
在[0,1]中的任意t
如果:f(tx+(1-t)y)≧tf(x) + (1-t)f(y)
那么這就是一個嚴謹的凹函式,當中x≠y和t是落於(0,1)。
某函式f:R→R,在x和y之間的每一點z,在圖中的點(z,f(z) )是在以點(x,f(x) ) and (y,f(y) )連成的直線之上。
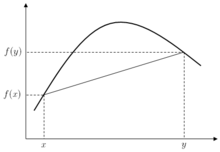 凹函式
凹函式性質
如果一個可微函式f它的導數f'在某區間是單調下跌的,f就是凹的:一個凹函式擁有一個下跌的斜率(當中下跌只是代表非上升而不是嚴謹的下跌,也代表這容許零斜率的存在。)
如果一個二次可微的函式f,它的二階導數f'(x)是正值(或者說它有一個正值的加速度),那么它的圖像是凸的;如果二階導數f'(x)是負值,圖像就會是凹的。當中如果某點轉變了圖像的凹凸性,這就是一個拐點。
如果凸函式(也就是向上開口的)有一個"底",在底的任意點就是它的極小值。如果凹函式有一個"頂點",那么那個頂點就是函式的極大值。
如果f(x)是二次可微的,那么f(x)就是凹的若且唯若f''(x)是非正值。如果二階導數是負值的話它就是嚴謹凹函式,但相反而言又不一定正確。
例子
函式和都是凹函式因為它們的二階導數永遠都是一個負值。
任何線性函式既是凸函式也是凹函式。
函式在區間是凹的。
函式是一個凹函式,當中是一個有定義矩陣的行列式。
凹函式性質的證明
設函式f(x)在定義域內連續可導且滿足f''(x)>0。
設x1<1
證明:f[ax1+(1-a)x2]
因ax1+(1-a)x2-x1=(1-a)(x2-x1)>0
則x1
根據拉格朗日中值定理。
必存在x1<μ>< ax1+(1-a)x2
使f[ax1+(1-a)x2]-f(x1)= (1-a)(x2-x1)f'(μ)
同理。
存在ax1+(1-a)x2<ξ>
使f(x2)- f[ax1+(1-a)x2]= a(x2-x1)f'(ξ)
故a{f[ax1+(1-a)x2]-f(x1)}- (1-a){f(x2)- f[ax1+(1-a)x2]}=a (1-a)(x2-x1)[f’(μ)- f’(ξ)]
根據拉格朗日中值定理。
有μ<δ><ξ>
f'(μ)- f'(ξ)=(μ-ξ)f''(δ)
因f''(x)>0
則f'(μ)- f'(ξ)<0
則a{f[ax1+(1-a)x2]-f(x1)}- (1-a){f(x2)- f[ax1+(1-a)x2]}<0
整理後得f[ax1+(1-a)x2]
若f''(x)<0結果相反 。
2]}=a (1-a)(x2-x1)[f’(μ)- f’(ξ)]
根據拉格朗日中值定理。
有μ<δ><ξ>
f'(μ)- f'(ξ)=(μ-ξ)f''(δ)
因f''(x)>0
則f'(μ)- f'(ξ)<0
則a{f[ax1+(1-a)x2]-f(x1)}- (1-a){f(x2)- f[ax1+(1-a)x2]}<0
整理後得f[ax1+(1-a)x2]
若f''(x)<0結果相反 。
注意:中國
某些機構關於函式凹凸性定義和國外的定義是相反的。Convex Function在某些中國大陸的數學書中指凹函式。Concave Function指凸函式。但在中國大陸涉及經濟學的很多書中,凹凸性的提法和其他國家的提法是一致的,也就是和數學教材是反的。舉個例子,同濟大學高等數學教材對函式的凹凸性定義與本條目相反,本條目的凹凸性是指其上方圖是凹集或凸集,而同濟大學高等數學教材則是指其下方圖是凹集或凸集,兩者定義正好相反。