單項式分組法簡介
就是指直接按標誌值的大小排列成組。標誌值按大小排列後,每個數量標誌值就是一個組,有多少個標誌值就分成多少個組。單項式分組其標誌值都是整數,如按產量分組、按技術級別、工齡等標誌分組,但在整數之間允許間斷。如標誌值為5、7、8、10件,有4個標誌值構成4個組,它們是不連續的整數。又如某小組的工人技術級別為3—7級工,它是5個標誌值構成單項式分組,其標誌是連續的整數。
單項式分組法用於標誌值變動範圍小、又少的狀況,如果標誌值較多,而且變動范圈又大,此時仍採用單項式分組,那必然會出現組數過多的現象,這樣不利於反映社會經濟現象的特徵及其規律性,此時可以採用組距式分組法 。
單項式分組的頻數統計
在統計分組中,落在不同小組中的數據個數為該組的頻數,各組的頻數之和等於這組數據的總數,通過對每組頻數的統計,可以看出數據的答題分布情況,根據分組標誌的特點,還可以通過頻數統計進行比較分析等方式認識數據。
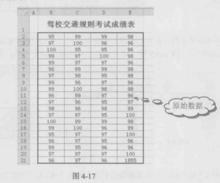 圖1
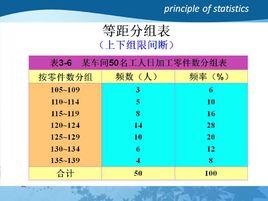
圖1如圖1所示,記錄了某次駕校交通規則考試中80名學員的考試成績,需要計算其頻數。從圖中可以看出表格中成績變化幅度不大,所以應該採用單項式分組法計算其頻數,可以將成績分為6組,分別為“95”、“96”、“97”、“98”、“99”和“100”。
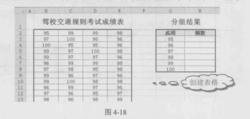 圖2
圖2(1)在工作表空白部分添加分組結果表格,並設定表格格式,如圖2所示。
 圖3
圖3(2)選中H3單元格,在公式編輯欄中輸入公式“=COUNTIF(B$2:E$21,G3)”,按Enter鍵,即可計算出成績為95分的考生人數,如圖3所示。
(3)選中H4單元格,在公式編輯欄中輸入公式“=COUNTIF(B$2:E$21,G4)”,按Enter鍵,即可計算出成績為96分的考生人數,如圖4所示。
 圖5
圖5(4)將游標定位到H4單元格右下角,向下拖動填充柄複製公式,即可計算出其他成績的考生人數,如圖5所示。
實驗數據的分組
 圖4
圖4實驗數據經檢查和核對後,可根據所得數據中所含變數的多少確定是否分組。當變數不多時(在30個以下的小樣本),不必分組,可直接進行統計分析。當變數較多時(一般在30個變數以上的大樣本),需要將變數分成若干組,以利於統計分析。數據經過分組歸類後,製成較有規則的次數分布表(圖),就可以初步看出數據的集中和變異情況,從而對數據有一個初步概念。對於不同類型的數據有不同的分類方法,現介紹如下:
1、連續性數據整理分組
連續性數據的分組是採用組距式分組法。在分組前先確定集差、組數、組距和組限等,然後將每個變數納入組內。
2、首先確定級差
找m所有計量數據中的最大值和最小值,最大值減最小值即為級差。即R=Max(x)-Min(x)
3、確定組數和組距
組數是根據樣本觀測數的多少及組距的大小來確定的,同時也要考慮到對資料需求的精確度及進一步計算是否方便。組距可以相等,也可不等。如果數據變動比較均勻,可採用等距分組,等距分組最大優點是各組的頻數(frequence)不受組距大小影響,一般均採用等距分組。當數據過分集中於一端。且相距甚遠(或出於描述事物特徵的需要以及保密的需要時),可採用不等距分組。
4、確定組限
組限是指每個組數值的起始點(下限值)和終止點(上限值),組內最大值為組上限,組內最小值為組下限。組上限=組下限+組距,如8~16、6~24、24~32、……。假定理論上分組時計入下限值,不計入上限值,則用這種方法分組後遇到16這樣的數可採用:各組上限為整數時減去0.1,小數一位時減去0.01,……,寫為8~15.9、6~23.9、24~31.9、……。對各組上限不記載,而用一短線表示,如8~、16~、24~、32~、……。
5、間斷性數據的整理分組
間斷性數據的整理分組基本採用單項式分組法,它是用樣本變數的自然值(或幾個變數值列為一組)進行分組,每組用一個變數值表示。分組時,將變數歸於相應的組內,然後製成次數分布表。通過對次數分布表的觀察以了解數據的集中和變異情況,便於進一步統計分析 。