概念
 單調映射
單調映射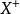 單調映射
單調映射 單調映射
單調映射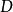 單調映射
單調映射 單調映射
單調映射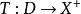 單調映射
單調映射單調遞增一元函式概念在對偶作用意義下的無窮維推廣,設 是巴拿赫空間, 為 的對偶空間, ⊂ , ,若有
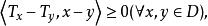 單調映射
單調映射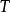 單調映射
單調映射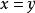 單調映射
單調映射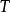 單調映射
單調映射則稱 為單調映射。若上式子中的等號僅當 時成立,則稱 為嚴格單調映射。若存在連續函式
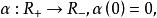 單調映射
單調映射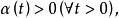 單調映射
單調映射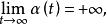 單調映射
單調映射使得
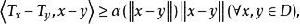 單調映射
單調映射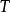 單調映射
單調映射則稱 為強單調映射。
基本原理
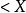 單調映射
單調映射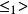 單調映射
單調映射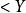 單調映射
單調映射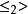 單調映射
單調映射 單調映射
單調映射 單調映射
單調映射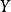 單調映射
單調映射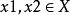 單調映射
單調映射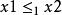 單調映射
單調映射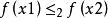 單調映射
單調映射 單調映射
單調映射 單調映射
單調映射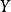 單調映射
單調映射定義:設 , , , 為有序集,稱函式 為 到 的單調映射。如果對任意 滿足 蘊含 ,則稱 為 到 的嚴格單調映射。
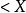 單調映射
單調映射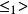 單調映射
單調映射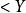 單調映射
單調映射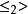 單調映射
單調映射 單調映射
單調映射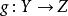 單調映射
單調映射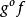 單調映射
單調映射 單調映射
單調映射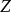 單調映射
單調映射定理:設 , , , 為有序集, , 為單調映射,那么 為 到 的單調映射。
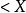 單調映射
單調映射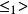 單調映射
單調映射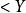 單調映射
單調映射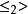 單調映射
單調映射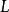 單調映射
單調映射 單調映射
單調映射 單調映射
單調映射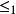 單調映射
單調映射 單調映射
單調映射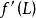 單調映射
單調映射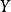 單調映射
單調映射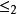 單調映射
單調映射定理:設 , , , 為有序集, ⊆ 為 中的 鏈, 為單調映射,那么 為 中的 鏈。

