簡介
對線性規劃的標準型:
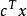 單純形表
單純形表min
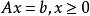 單純形表
單純形表s.t.
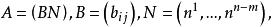 單純形表
單純形表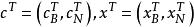 單純形表
單純形表 單純形表
單純形表記一個基礎可行解的基為 B , A 其餘的列為 N , 相應地,記 。有
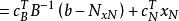 單純形表
單純形表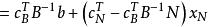 單純形表
單純形表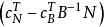 單純形表
單純形表這是一個很重要的式子,說明了對一個非基變數,僅當量 為負時,才有可能變成新的基變數。這些係數在下面的單純形表中稱為判別數或檢驗數。
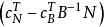 單純形表
單純形表當 全部大於等於零時,已經是最優基。對基 B ,以下的表稱為單純形表:
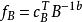 單純形表 單純形表 | 0 (基變數判別數) | 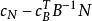 單純形表 單純形表 |
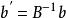 單純形表 單純形表 | 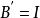 單純形表 單純形表 | 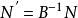 單純形表 單純形表 |
舉例
設有線性規劃問題如下:
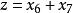 單純形表
單純形表min
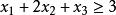 單純形表
單純形表s.t.
 單純形表
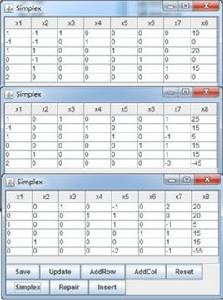
單純形表其對應的單純形表為:
| max | 0 | 0 | 0 | 0 | 0 | -1 | -1 | RHS |
| x₁ | x₂ | x₃ | x₄ | x₅ | x₆ | x₇ | ||
| x₆ | 1 | 2 | 1 | -1 | 0 | 1 | 0 | 3 |
| x₇ | 2 | -1 | 3 | 0 | -1 | 0 | 1 | 4 |
| 檢驗數σ | 3 | 1 | 4 | -1 | -1 | 0 | 0 | |
| x₆ | 1/3 | 7/3 | 0 | -1 | 1/3 | 1 | -1/3 | 5/3 |
| x₃ | 2/3 | -1/3 | 1 | 0 | -1/3 | 0 | 1/3 | 4/3 |
| 檢驗數σ | 1/3 | 7/3 | 0 | -1 | 1/3 | 0 | -4/3 | |
| x₂ | 1/7 | 1 | 0 | -3/7 | 1/7 | 3/7 | -1/7 | 5/7 |
| x₃ | 5/7 | 0 | 1 | -1/7 | -2/7 | 1/7 | 2/7 | 11/7 |
| 檢驗數σ | 0 | 0 | 0 | 0 | 0 | -1 | -1 | |
| x₂ | 1/7 | 1 | 0 | -3/7 | 1/7 | 3/7 | -1/7 | 5/7 |
| x₃ | 5/7 | 0 | 1 | -1/7 | -2/7 | 1/7 | 2/7 | 11/7 |
| 檢驗數σ | 0 | 0 | 0 | 0 | 0 | -1 | -1 |