詳細概念
單參數變換群(one-para meter group of trans-formations)亦稱R在流形上的(左)作用。黎曼幾何的一個概念。流形上的一族微分同胚。C流形M上的單參數變換群是M的一族C微分同胚{φ}(t∈R)，它具有以下性質：
1.φ：R×M→M， (t，p)→φ(p)是C映射。
2. φ：M→M是恆同映射。
3. φ°φ=φ
若U是M的一個開鄰域，I=(-ε，ε)，以I×U來替代R×M且使t，s，t+s∈I，則{φ}稱為作用在U上的局部單參數變換群。這時φ：U→φ(U)是C微分同胚。
對於局部單參數變換群{φ}及U中的任一點p，由t→φ(p)定義的映射γ：I→M是M中過p的一條參數曲線。它稱為群{φ}過p點的軌線，以X表示軌線γ(t)=φ(p)在p點的切向量，即：
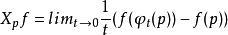單參數變換群這樣就在U上給定了一個C向量場X，它稱為由{φ}誘導的向量場。因為(φ)X=X=X，即(φ)X=X，所以{φ}的軌線都是其誘導的向量場的積分曲線，並且誘導向量場X在每個微分同胚φ下是不變的。對於M上的單參數變換群有相同的結論。反之，若給定一個M上的C向量場Y，則有：對M的任一點p，必存在含p的一個鄰域U及作用在U上的局部單參數群{φ}，使得在U上Y|U是由{φ}誘導的向量場。因此，也稱Y是局部單參數變換群{φ}的無窮小生成元，或簡單地說Y生成{φ}。當M是緊緻連通流形時U=M，從而緊緻C流形M上的C向量場是一個單參數變換群的無窮小生成元。
群
群是一種只有一個運算的、比較簡單的代數結構；是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合，a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”，運算結果稱為“乘積”)滿足：
(1)封閉性，a·b∈G;
(2)結合律，即(a·b)c = a·(b·c);
(3)對G中任意元素a、b，在G中存在惟一的元素x，y，使得a·x= b，y·a=b，則稱G對於所定義的運算“·”構成一個群。例如，所有不等於零的實數，關於通常的乘法構成一個群;時針轉動(關於模12加法)，構成一個群。
滿足交換律的群，稱為交換群。
群是數學最重要的概念之一，已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱，就存在群。例如，可以用研究圖形在變換群下保持不變的性質，來定義各種幾何學，即利用變換群對幾何學進行分類。可以說，不了解群，就不可能理解現代數學。
1770年，拉格朗日在討論代數方程根之間的置換時，首先引入群的概念，而它的名稱，是伽羅華在1830年首先提出的。
同胚
拓撲空間之間的一種變換。若f是拓撲空間(X，T)到(Y，U)的單滿映射，並且f與f都是連續的，則稱f為同胚映射或拓撲變換。存在同胚映射的兩個拓撲空間稱為同胚的或拓撲等價的。同胚關係是等價關係。抽象空間的同胚是弗雷歇(Fréchet，M.-R.)於1910年開始研究的。在狹窄的意義下同胚的概念早已被龐加萊(Poincaré，(J.-)H.)引入。
微分同胚
微分同胚是微分流形之間的一類同胚映射。它與它的逆映射都是可微的.設M，N均為微分流形，對於映射f：M→N，若f是同胚映射，並且f，f都是C可微映射，則稱f為M到N上的C微分同胚。C微分同胚f：M→N簡稱M到N上的微分同胚。對於微分流形M，N，若存在(C)微分同胚f：M→N，則稱M與N是(C)微分同胚的微分流形，記為MN.“”是微分拓撲學中的基本等價關係。微分拓撲的基本任務是研究微分流形在微分同胚下保持不變的性質，以及尋求在怎樣的條件下兩個微分流形是微分同胚的。米爾諾(Milnor，J.W.)於1956年證明，在S上至少存在兩個不微分同胚的微分構造。後來證實，S上恰好有15個這樣的不同的微分構造。
黎曼幾何
微分幾何的一個重要分支，由德國數學家黎曼(Riemann，(G.F.)B.)於19世紀中期所開創。他於1854年在哥丁根大學所做的就職演說“關於幾何學基礎的假設”是黎曼幾何的發端。後經克里斯托費爾(Christoffel，E.B.)、里奇(Ricci，C.G.)、列維-齊維塔(Levi-Civita，T.)等人進一步完善和發展，成為愛因斯坦(Einstein，A.)於1905年創立廣義相對論的有力數學工具，也使黎曼幾何得以蓬勃發展。嘉當(Cartan，E.)建立的外微分形式和活動標架法，使李群與黎曼幾何溝通起來，為黎曼幾何的發展開闢了廣闊的前途，影響極為深遠。近半個世紀以來，黎曼幾何的研究從“局部”發展到“整體”，產生了許多深刻的並在其他數學分支(如拓撲學、偏微分方程論、多複變函數論等)及理論物理中有重要影響的結果。現在，黎曼幾何已成了現代數學的重要內容之一。
黎曼幾何是黎曼流形上的幾何學，黎曼流形是局部歐氏化的微分流形。設M是n維微分流形，若在每點p∈M的切空間中給定一個光滑依賴於p的歐氏度量g(即正定數積)，則(M，g)就成為黎曼流形，g稱為黎曼度量。當g與點p無關時，就得到通常的歐氏空間。黎曼的傑出創造之處就在於把度量看成是附加到流形上去的一個結構，一個流形可賦予眾多的黎曼度量。
