基本概念
表示方法
兩個向量 a和 b的叉積寫作 a× b(有時也被寫成 a∧ b,避免和字母x混淆)。
定義
向量積可以被定義為:。
模長:(在這裡θ表示兩向量之間的夾角(共起點的前提下)(0°≤θ≤180°),它位於這兩個矢量所定義的平面上。)
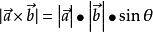 向量積
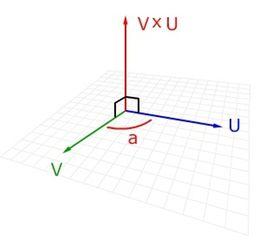
向量積方向:a向量與b向量的向量積的方向與這兩個向量所在平面垂直,且遵守右手定則。(一個簡單的確定滿足“右手定則”的結果向量的方向的方法是這樣的:若坐標系是滿足右手定則的,當右手的四指從 a以不超過180度的轉角轉向 b時,豎起的大拇指指向是 c的方向。)
也可以這樣定義(等效):
向量積| c|=| a× b|=| a|| b|sin< a,b>
即 c的長度在數值上等於以 a, b,夾角為θ組成的平行四邊形的面積。
而 c的方向垂直於a與b所決定的平面, c的指向按右手定則從a轉向b來確定。
*運算結果 c是一個偽向量。這是因為在不同的坐標系中 c可能不同。
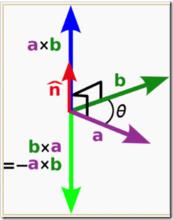 向量積
向量積坐標運算
設=(),=()。i,j,k分別是X,Y,Z軸方向的單位向量,則 :
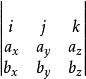 向量積
向量積a× b=(-) i+(-) j+(-) k,為了幫助記憶,利用三階行列式,寫成det
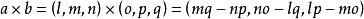 向量積
向量積證明
為了更好地推導,我們需要加入三個軸對齊的單位向量i,j,k。
i,j,k滿足以下特點:
i=jxk;j=kxi;k=ixj;
kxj=–i;ixk=–j;jxi=–k;
ixi=jxj=kxk=0;(0是指0向量)
由此可知,i,j,k是三個相互垂直的向量。它們剛好可以構成一個坐標系。
這三個向量的特例就是i=(1,0,0)j=(0,1,0)k=(0,0,1)。
對於處於i,j,k構成的坐標系中的向量u,v我們可以如下表示:
u=Xu*i+Yu*j+Zu*k;
v=Xv*i+Yv*j+Zv*k;
那么uxv=(Xu*i+Yu*j+Zu*k)x(Xv*i+Yv*j+Zv*k)
=Xu*Xv*(ixi)+Xu*Yv*(ixj)+Xu*Zv*(ixk)+Yu*Xv*(jxi)+Yu*Yv*(jxj)+Yu*Zv*(jxk)+Zu*Xv*(kxi)+Zu*Yv*(kxj)+Zu*Zv*(kxk)
由於上面的i,j,k三個向量的特點,所以,最後的結果可以簡化為
uxv=(Yu*Zv–Zu*Yv)*i+(Zu*Xv–Xu*Zv)*j+(Xu*Yv–Yu*Xv)*k。
與數量積的區別
註:向量積≠向量的積(向量的積一般指點乘)
一定要清晰地區分開向量積(矢積)與數量積(標積)。見下表。
| 名稱 | 標積/內積/數量積/點積 | 矢積/外積/向量積/叉積 |
| 運算式(a,b和c粗體字,表示向量) | a·b=|a||b|·cosθ | a×b=c,其中|c|=|a||b|·sinθ,c的方向遵守右手定則 |
| 幾何意義 | 向量a在向量b方向上的投影與向量b的模的乘積 | c是垂直a、b所在平面,且以|b|·sinθ為高、|a|為底的平行四邊形的面積 |
| 運算結果的區別 | 標量(常用於物理)/數量(常用於數學) | 矢量(常用於物理)/向量(常用於數學) |
性質
幾何意義及其運用
叉積的長度| a× b|可以解釋成這兩個叉乘向量 a, b共起點時,所構成平行四邊形的面積。據此有:混合積[ a b c]=( a× b)· c可以得到以 a, b, c為棱的平行六面體的體積。
代數規則
1、反交換律:a×b=-b×a
2、加法的分配律:a×(b+c)=a×b+a×c。
3、與標量乘法兼容:(ra)×b=a×(rb)=r(a×b)。
4、不滿足結合律,但滿足雅可比恆等式:a×(b×c)+b×(c×a)+c×(a×b)=0。
5、分配律,線性性和雅可比恆等式別表明:具有向量加法和叉積的R3構成了一個李代數。
6、兩個非零向量a和b平行,若且唯若a×b=0。
拉格朗日公式
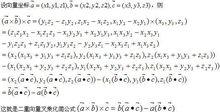 證明過程
證明過程這是一個著名的公式,而且非常有用:
(a× b)× c= b( a· c)- a( b· c)
a×( b× c)= b( a· c)- c( a· b)
證明過程如下:
二重向量叉乘化簡公式及證明
可以簡單地記成“BAC-CAB”。這個公式在物理上簡化向量運算非常有效。需要注意的是,這個公式對微分運算元不成立。
這裡給出一個和梯度相關的一個情形:
這是一個霍奇拉普拉斯運算元的霍奇分解的特殊情形。
另一個有用的拉格朗日恆等式是:
這是一個在四元數代數中範數乘法|vw|=|v||w|的特殊情形。
矩陣形式
給定直角坐標系的單位向量i,j,k滿足下列等式:
i×j =k;
j×k=i;
k×i=j;
通過這些規則,兩個向量的叉積的坐標可以方便地計算出來,不需要考慮任何角度:設
a=[a1,a2,a3]=a1i+a2j+a3k;
b=[b1,b2,b3]=b1i+b2j+b3k;
則a×b=[a2b3-a3b2,a3b1-a1b3,a1b2-a2b1]。
叉積也可以用四元數來表示。注意到上述i,j,k之間的叉積滿足四元數的乘法。一般而言,若將向量[a1,a2,a3]表示成四元數a1i+a2j+a3k,兩個向量的叉積可以這樣計算:計算兩個四元數的乘積得到一個四元數,並將這個四元數的實部去掉,即為結果。更多關於四元數乘法,向量運算及其幾何意義請參看四元數(空間鏇轉)。
高維情形
七維向量的叉積可以通過八元數得到,與上述的四元數方法相同。
七維叉積具有與三維叉積相似的性質:
雙線性性:x×(ay+bz)=ax×y+bx×z;(ay+bz)×x=ay×x+bz×x;
反交換律:x×y+y×x=0;
同時與x和y垂直:x·(x×y)=y·(x×y)=0;
拉格朗日恆等式:|x×y|²=|x|²|y|²-(x·y)²;
不同於三維情形,它並不滿足雅可比恆等式:x×(y×z)+y×(z×x)+z×(x×y)≠0。
套用
在物理學光學和計算機圖形學中,叉積被用於求物體光照相關問題。
求解光照的核心在於求出物體表面法線,而叉積運算保證了只要已知物體表面的兩個非平行矢量(或者不在同一直線的三個點),就可依靠叉積求得法線。