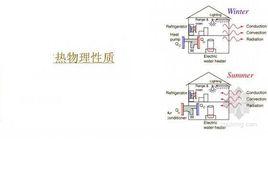
簡介
熱的概念來自人們對冷熱的感覺。它是物質運動表現的形式之一。它的本質是大量的實物粒子(分子、原子等)永不停息地作無規則的運動。熱與實物粒子的無規則運動的速度有關,無規則運動越強烈時,則該物體或系統就越熱,溫度也越高。熱的另一種涵義是熱量,熱量是能量變化的一種量度。熱量與溫度的概念不同,不能混為一談。熱運動是物質的一種運動形式。巨觀物體內部大量微觀粒子(如分子、原子、電子等)永不停息的無規則運動稱為熱運動。它是物質的一種基本運動形式。一個物體或某一系統在熱平衡時的溫度,取決於他內部微觀粒子熱運動的狀況,熱運動越劇烈,它的溫度就越高。凡與溫度有關的物質系統性質的變化,統稱為“熱現象”
分類
熱力學和統計物理學研究對象是一致的,都是研究物體內部熱運動的規律性以及熱運動對物體性質的影響,但是研究的方法截然不同。熱力學根據觀察和實驗所總結出來的熱力學定律,以嚴密的邏輯推理來研究巨觀物體的熱性質,它不涉及物質的微觀結構。統計物理學則從物質的微觀結構出發,依據每個粒子所遵循的力學規律,用統計學的方法研究巨觀物體的熱性質。熱力學對熱現象給出可靠的依據,用以驗證微觀理論的正確性;統計物理學可深入探討熱現象的本質,使熱力學的理論獲得更深刻的意義。因此這兩種方法,起到了相輔相成的作用,使熱現象的研究更加深入。
熱力學
它是研究熱現象中物態轉變和能量轉換的學科。由觀察和實驗總結出熱現象的規律,構成熱現象的巨觀理論。在19世紀中葉,焦耳等人通過多次實驗,將熱確定為能的一種形式,從而建立了熱力學。熱力學的研究是從大量經驗中總結了自然界有關熱現象的一些共同規律而得出熱力學定律(即熱力學第零、第一、第二和第三定律),用嚴密的邏輯推理來研究巨觀物體的熱性質及規律。通常是將熱力學第一定律及第二定律視作熱力學的基本定律,但有時增加能斯特定理當作第三定律,又有時將溫度存在定律當作第零定律。一般將這四條熱力學規律統稱為熱力學定律。熱力學是熱現象的巨觀理論,它是以這四條定律為基礎建立起來的理論。
熱力學第零定律
若兩個熱力學系統中的任何一個系統都和第三個熱力學系統處於熱平衡狀態,那么,這兩個熱力學系統也必定處於熱平衡。這一結論稱做“熱力學第零定律”。熱力學第零定律的重要性在於它給出了溫度的定義和溫度的測量方法。定律中所說的熱力學系統是指由大量分子、原子組成的物體或物體系。它為建立溫度概念提供了實驗基礎。這個定律反映出:處在同一熱平衡狀態的所有的熱力學系統都具有一個共同的巨觀特徵,這一特徵是由這些互為熱平衡系統的狀態所決定的一個數值相等的狀態函式,這個狀態函式被定義為溫度。而溫度相等是熱平衡之必要的條件。因此,這一基本物理量實質是反映了系統的某種性質。
在熱力學第一定律建立以前,人們曾幻想製造出一種永動的機器,不需要任何燃料和動力,又不消耗系統本身的內能,卻能不斷對外做功而且永遠運轉,這類機器叫“第一類永動機”。根據能的轉化與守恆定律,系統在對外做功過程中,它的內能要減小,要想不減少它的內能,外界必須同時對它傳遞熱量或對它做功,不斷地給系統補充能量,系統才能持續不斷地對外做功。這種違背能量守恆與轉化定律的器械,也就是違背熱力學第一定律的器械永遠也不可能製造成。
熱力學第一定律
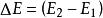 熱物理性質
熱物理性質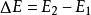 熱物理性質
熱物理性質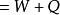 熱物理性質
熱物理性質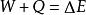 熱物理性質
熱物理性質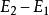 熱物理性質
熱物理性質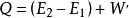 熱物理性質
熱物理性質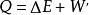 熱物理性質
熱物理性質是熱力學的基本定律之一。是能的轉化與守恆定律在熱力學中的表現。它指出熱是物質運動的一種形式,並表明,一個體系內能增加的量值 等於這一體系所吸收的熱量Q 與外界對它所做的功之和,可表示為 即 。在這個公式中,突出了做功和熱傳遞是改變系統內能的兩種不同形式,可通過做功和被傳遞的熱量來量度系統內能的變化。在上述公式中,當外界對系統作功時,W為正值;若系統對外作功時,W 為負值。如外界向系統傳熱,Q 即為正值;若系統向外界放熱,則Q 為負值。當△E 為正值時,表示系統的內能增加;如果△E 為負值時,則表現系統的內能在減少。對熱力學第一定律也可以從另一側面來描述,即外界傳遞給系統的熱量等於系統內能的增量和系統對外所作的功的總和。如果外界傳遞給系統的熱量為Q,使系統從某一平衡狀態到達另一平衡狀態,內能的增加為 ,同時對外作功W′,則熱力學第一定律可表示為 即 。在這個公式中,當系統從外界獲得熱量時,Q>0為正值;而當系統向外界釋放熱量時, Q0為正值;若外界對系統作功,W′<0為負值。在系統內能增加時,△E 為正值,若系統的內能減少時,則△E 為負值。
熱力學第二定律
熱力學的基本定律之一。它是關於在有限空間和時間內,一切和熱運動有關的物理、化學過程具有不可逆性的總結。克勞修斯、開爾文等人,從將熱轉變為功時遇到的經驗歸納成熱力學第二定律。它實質上指出了巨觀熱現象的不可逆性。它的表述有很多種,但實際上都是互相等效的。如下列幾種表述:
克勞修斯表述:克勞修斯在1850年提出的。熱量總是自動的從高溫物體傳到低溫物體,不可能自動地由低溫物體向高溫物體傳遞。在它的表述中,指出在自然條件下熱量只能從高溫物體向低溫物體轉移,而不能由低溫物體自動向高溫物體轉移,這個轉變過程是不可逆的。若想讓熱傳遞方向逆轉,則必須消耗功才能實現。
2.開爾文表述:開爾文在1851年提出的。不存在這樣一種循環過程,系統從單一熱源吸取熱量,使之完全變為有用功而不產生其他影響。表述中的“單一熱源”是指溫度均勻並且恆定不變的熱源;“其他影響”指除了由單一熱源吸熱,把所吸的熱用來作功以外的任何其他變化。若有其他影響產生時,把由單一熱源吸來的熱量全部用來對外作功是可能的。自然界中任何形式的能都可能轉變成熱,但熱卻不能在不產生其他影響的條件下完全變成其他形式的能,這種轉變在自然條件下也是不可逆的。熱機在運行過程中,可連續不斷地將熱變為機械功,一定伴隨有熱量的損失。第二定律和第一定律兩者有所不同。第二定律闡明了過程進行的方向性。
根據熱力學第零定律,確定了態函式——溫度;根據熱力學第一定律,確定了態函式——內能和焓;根據熱力學第二定律,也可以確定一個新的態函式——熵。可以用熵來對第二定律作定量的表述。
熱力學第二定律在引入熵的概念後,可用數學形式表示。其積分形式為
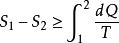 熱物理性質
熱物理性質式中不等號對應於不可逆過程,等號對應於可逆過程,角碼1和2分別表示系統的初狀態和末狀態,S 表示系統的熵。熱力學第二定律的微分形式
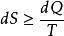 熱物理性質
熱物理性質式中不等號對應於不可逆過程,等號對應於可逆過程。在孤立系統內對可逆過程,系統的熵總保持不變;對不可逆過程,系統的熵總是增加的。這個規律叫做熵增加原理。熵的增加表示系統從幾率小的狀態向幾率大的狀態演變,也就是從比較有規則、有秩序的狀態向更無規則、更無秩序的狀態演變。
熱力學第三定律
此定律指出,構想通過幾個有限的步驟使物體冷卻到絕對零度,是不可能的。這一表述是能斯脫於1912年根據對低溫現象的研究得出能斯脫定理的推論。
統計物理學
是用統計方法研究由大量微觀粒子組成的物質系統內部熱運動規律及其對系統性質的影響。它是從物質的微觀結構,即從分子、原子的運動和它們之間的相互作用出發,來研究熱現象的規律,構成熱現象的微觀理論。統計物理學的前身是氣體分子運動論。統計物理學是從巨觀系統內部的微觀結構出發,根據微觀粒子所遵從的力學規律,用統計方法,將系統的巨觀性質及其變化規律推導出來。所以,統計物理學與熱力學兩者之間可以相互補充。
理想氣體
把嚴格服從波義耳-馬略特定律、蓋·呂薩克定律和查理定律的想像的氣體,稱為“理想氣體”。氣體分子運動論的研究對象主要是氣體物質系統。在通常情況下,氣體中的分子本身所占的體積,比起氣體分子所能自由活動的空間,即氣體的體積是小得多的,所以分子本身的大小可忽略不計。例如,在溫度為0℃、壓強為1大氣壓下的氣體,其密度不到液體的密度的千分之一。在某種情況下忽略氣體分子本身的大小對我們研究的問題影響並不大。若在高溫低壓的情況下,將氣體分子本身的大小忽略掉,則影響就更小。至於氣體分子之間的相互作用力,由於它隨著分子之間距離的增大而迅速地減小,故在一般常溫、常壓下,也可忽略不計氣體分子之間存在著的分子力。也就是說,除了氣體分子之間發生碰撞的瞬間之外,可認為氣體分子之間是沒有相互作用的。此外,也不考慮氣體分子的內部結構,即認為分子在碰撞過程中不發生形變。若將氣體分子視為剛體,而分子間的碰撞又是完全彈性碰撞,那么,氣體分子就遵守動量守恆和動能守恆定律。符合上述要求的氣體即稱為理想氣體。在通常的溫度和壓強下,理想氣體和實際氣體的性質差別並不太大。因此,所有的實際氣體在溫度不太低、壓強不太大的情況下,都可近似地看作理想氣體。
玻義耳-馬略特定律:
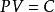 熱物理性質
熱物理性質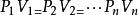 熱物理性質
熱物理性質它反映氣體的體積隨壓強改變而改變的規律。對於一定質量的氣體,在其溫度保持不變時,它的壓強和體積成反比;或者說,其壓強P 與它的體積V 的乘積為一常量,即(常數)(T 不變時)或式中常量的大小與氣體系統的溫度和氣體的質量有關。實際氣體只是在壓強不太高、溫度不太低的條件下才服從這一定律。
蓋·呂薩克定律:
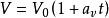 熱物理性質
熱物理性質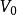 熱物理性質
熱物理性質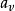 熱物理性質
熱物理性質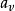 熱物理性質
熱物理性質它反映了氣體體積隨溫度變化而變化的規律。一定質量的氣體,在保持壓強不變的情況下,它的體積變化與溫度變化成正比,與0℃時的體積成正比,即它的體積隨著溫度作直線變化,其數學表達式為。式中V 為氣體在t℃時的體積;為0℃時的體積; 是在壓強不變時,氣體體積隨溫度變化的係數,稱做體膨脹係數。可由實驗測定。
查理定律:
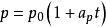 熱物理性質
熱物理性質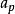 熱物理性質
熱物理性質它反映了氣體壓強隨溫度變化而變化的規律。一定質量的氣體,當其體積保持不變時,它的壓強P 變化與溫度T 的變化成正比,與0℃時氣體的壓強成正比,即壓強隨溫度作直線變化,其數學表達式為。式中P 為氣體在t℃時的壓強;P0為氣體在0℃時的壓強; 為體積不變時,氣體壓強隨溫度變化的係數,稱作壓強係數。
理想氣體狀態方程
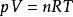 熱物理性質
熱物理性質波義耳-馬略特定律,蓋·呂薩克定律及查理定律給出了一定質量的氣體的三個參量P、V、T 中有一個保持不變時,另兩個狀態參量的變化規律。但是,在實際中,這三個參量往往是同時變化的。對於一定質量的理想氣體,在平衡狀態下,壓強P、體積V 和溫度T 之間存有一定的關係,可用兩種形式來表示。其一是式中角碼1和2分別代表系統所處的兩個平衡態。其二是或者寫成。式中M、n和μ分別是氣體的質量、摩爾數和摩爾質量,R 為普適氣體常數。這種形式亦稱為克拉珀龍方程。以上兩種形式都是理想氣體狀態方程。理想氣體狀態方程表明:一定質量的氣體,當其狀態發生變化時,它的任意兩個平衡態的狀態參量之間的關係。對一定質量的氣體,P、V、T 三個狀態參量,並不全是獨立的,任何兩個參量確定之後,第三個參量也就唯一地確定了,只需兩個獨立參量,即可描述理想氣體的狀態。