概念
在拓撲學中, 同胚(homeomorphism、topological isomorphism、bi continuous function)是兩個拓撲空間之間的雙連續函式。同胚是拓撲空間範疇中的同構;也就是說,它們是保持給定空間的所有拓撲性質的映射。如果兩個空間之間存在同胚,那么這兩個空間就稱為 同胚的,從拓撲學的觀點來看,兩個空間是相同的。
大致地說,拓撲空間是一個幾何物體,同胚就是把物體連續延展和彎曲,使其成為一個新的物體。因此,正方形和圓是同胚的,但球面和環面就不是。有一個笑話是說,拓撲學家不能區分咖啡杯和甜甜圈,這是因為一個足夠柔軟的甜甜圈可以捏成咖啡杯的形狀。
在拓撲學中,兩個流形,如果可以通過彎曲、延展、剪下(只要最終完全沿著當初剪開的縫隙再重新貼上起來)等操作把其中一個變為另一個,則認為兩者是同胚的。如:圓和正方形是同胚的,而球面和環面就不是同胚的。
定義
兩個拓撲空間{ X, T}和{ Y, T}之間的函式 f: X→ Y稱為 同胚,如果它具有下列性質:
•f是雙射(單射和滿射);
•f是連續的;
•反函式f也是連續的(f是開映射)。
滿足以上三個性質的函式有時稱為 雙連續。 自同胚就是從一個拓撲空間到它本身的同胚。同胚形成了所有拓撲空間的類上的等價關係。所得到的等價類稱為 同胚類。
例子
R內的單位圓盤D和單位正方形是同胚的。
開區間(−1, 1)與實直線 R同胚。
積空間S× S與二維環面同胚。
每一個一致同構和等距同構都是同胚。
任何二維球面去掉一個點都與 R中的所有點所組成的集合(二維平面)同胚。
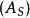 同胚
同胚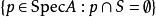 同胚
同胚設A為一個有單位的交換環,並設S為A的乘法子集。那么Spec與同胚。
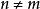 同胚
同胚 同胚
同胚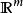 同胚
同胚當時,不與同胚。
一個連續和雙射但不是同胚的函式的例子,是把半開區間 [0,1)纏繞到圓上的映射。在這個情況中,逆映射雖然存在,但不是連續的。
性質
•同胚是拓撲空間範疇中的同構。因此,兩個同胚的複合映射也是同胚,且所有自同胚X→X形成了一個群,稱為X的自同胚群,通常記為Homeo(X)。
•兩個同胚的空間具有相同的拓撲性質。例如,如果其中一個是緊空間,那么另外一個也是緊空間;如果其中一個是連通空間,那么另外一個也是連通空間,等等。然而,這不能推廣到通過度量所定義的性質;如果兩個度量空間是同胚的,那么仍然有可能其中一個是完備的,而另外一個不是。
•同胚既是開映射又是閉映射,也就是說,它把開集映射到開集,把閉集映射到閉集。
•每一個S的自同胚都可以延伸到整個圓盤D的自同胚。
參見
•局部同胚
•微分同胚
•一致同構(一致空間的同構)
•等距同構(度量空間的同構)
•同胚 (圖論)(與圖的剖分有密切聯繫)
•同痕
•映射類群

