基本假設
同方差性有四個基本假設 ,假設一被稱為(White Noise Condition)白色噪音假設, 干擾項為No Autocorrelation;即誤差部分相互沒有關聯,假設回歸式 y = α+βx+u, 其誤差項中,u1,u2各誤差之間沒有任何聯繫,即:COV(u1*u2)=0;假設二為干擾項具備同方差性或者等分散, 即誤差項與獨立變數(independent variable)之間相互獨立, 並且誤差項的分散(方差 Variance)必須等同,即Var(u|x)=σ^2;解釋變數之間不存在多重共線性;解釋變數是確定變數。
求證過程
在滿足上述要求的前提下,OLS回歸式的統計量才能夠同時滿足不偏性Unbaisedness和效率性Efficiency。所推定出來的線性回歸式才能被稱為最好的不偏線性統計量(BLUE; best linear unbaised estimators)。
等方差性條件下不偏性和OLS斜率值的求證:
所有線性回歸式可以表現為矩陣(Matrix)y=xβ+e 其中y為n*1, x為n*k, e為n*1。
根據OLS, S=∑e^2=∑e'*e. FOC β on S==> -2x'(y-βx)=0 ==> β=(x'x)^-1x'e=β+(x'x)^-1x'e
不偏性
Unbiasedness,不偏性
E(β) = β+E(x'x)^-1x'e)=β+E[E(x'x)^-1x'e|x)]=β+E((x'x)^-1x'E(e|x)]=β
推定
最好的不偏性統計量(BLUE)
假設單純回歸式y=α+βx+u滿足white noise condition的2個假設即,No autocorrelation和同方差性,以及Gauss Markov condition,β的分散可定義為Var(β^)=σ∑w^2. 假設有另一個統計量β~滿足線性式。 求證:Var(β^)<Var(β~)
β~=∑w~*y since β satisfies the condition of linear estimator. ==> β~=∑w~*(α+βx+u)=α∑w~+β∑w~*x+∑w~*u 為了滿足不偏性,這裡∑w~*x=1 由此可得出β~的方差:Var(β~)=σ^2∑w~^2。想要證明Var(β^)<Var(β~) 必須得出∑w~^2>∑w^2. 在要求不偏性的時候已經得出∑w~*x=1,所以可推定∑w~*w=1,進而得出 ∑w~^2-∑w^2=(∑w~^2-∑w^2)^2>0==>∑w~^2>∑w^2即Var(β^)<Var(β~)。
同方差性檢驗
誤差項的同方差性檢驗一般運用E檢驗,即能量檢驗(Energy Test),計算機率分布之間的統計學概念下的距離。
其他檢驗包括:Breush-Pagan檢驗 ,對平方後的誤差項運行一個輔助回歸,保留被解釋的平方項的和,通過開方檢驗判斷誤差項是否具有異方差性。其替代檢驗:Koenker-Bassett檢驗則在樣本量較小時套用。
判斷同方差性實例:
用EVIEWS測定是否符契約方差(存在異方差Heteroskedasticity)- Heteroskedasticity test (White)
Heteroskedasticity Test: Breusch-Pagan-Godfrey
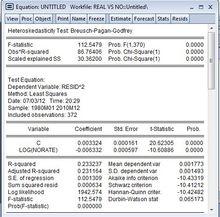 同方差性
同方差性套用
同方差性主要套用於原始數據圖形模式識別及機器學習算法研究;
費舍的線性判別分析,試圖找到兩類物體或事件的特徵的一個線性組合,以能夠特徵化或區分它們。
1.同方差性主要套用於原始數據圖形模式識別及機器學習算法研究;
2.費舍的線性判別分析,試圖找到兩類物體或事件的特徵的一個線性組合,以能夠特徵化或區分它們。

