概念介紹
可除代數(division algebra)平行於除環的一類重要代數。若R代數A的每個非零元在A中恆有逆元,即A* =A\{0}是乘群,則稱A是R可除代數。R是域時,R可除代數簡稱可除代數。代數閉域F上有限維可除代數只有F自身。而實數域R上有限維可除代數有且僅有實數域、複數域與四元數可除代數三種,這是有限維可除代數著名的弗羅貝尼烏斯結構定理。
代數
代數是數學的一個分支。傳統的代數用有字元 (變數) 的表達式進行算術運算,字元代表未知數或未定數。如果不包括除法 (用整數除除外),則每一個表達式都是一個含有理係數的多項式。例如: 1/2 xy+1/4z-3x+2/3. 一個代數方程式 (參見EQUATION)是通過使多項式等於零來表示對變數所加的條件。如果只有一個變數,那么滿足這一方程式的將是一定數量的實數或複數——它的根。一個代數數是某一方程式的根。代數數的理論——伽羅瓦理論是數學中最令人滿意的分支之一。建立這個理論的伽羅瓦(Evariste Galois,1811-32)在21歲時死於決鬥中。他證明了不可能有解五次方程的代數公式。用他的方法也證明了用直尺和圓規不能解決某些著名的幾何問題(立方加倍,三等分一個角)。多於一個變數的代數方程理論屬於代數幾何學,抽象代數學處理廣義的數學結構,它們與算術運算有類似之處。參見,如: 布爾代數(BOOLEAN ALGEBRA);群 (GRO-UPS);矩陣(MATRICES);四元數(QUA-TERNIONS );向量(VECTORS)。這些結構以公理 (見公理法 AXIOMATICMETHOD) 為特徵。特別重要的是結合律和交換律。代數方法使問題的求解簡化為符號表達式的操作,已滲入數學的各分支。
設K為一交換體. 把K上的向量空間E叫做K上的代數,或叫K-代數,如果賦以從E×E到E中的雙線性映射.換言之,賦以集合E由如下三個給定的法則所定義的代數結構:
——記為加法的合成法則(x,y)↦x+y;
——記為乘法的第二個合成法則(x,y)↦xy;
——記為乘法的從K×E到E中的映射(α,x)↦αx,這是一個作用法則;
這三個法則滿足下列條件:
a) 賦以第一個和第三個法則,E則為K上的一個向量空間;
b) 對E的元素的任意三元組(x,y,z),有
x(y+z)=xy+xz(y+z)x=yx+zx;
c)對K的任一元素偶(α,β)及對E的任一元素偶(x,y),有(αx)(βy)=(αβ) (xy).
設A為一非空集合. 賦予從A到K中的全體映射之集ℱ(A,K)以如下三個法則:
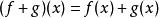 可除代數
可除代數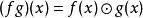 可除代數
可除代數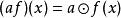 可除代數
可除代數則ℱ(A, K)是K上的代數, 自然地被稱為從A到K中的映射代數。當A=N時, 代數ℱ(A,K)叫做K的元素序列代數。
無論是在代數還是在分析中,代數結構都是最常見到的結構之一。十九世紀前半葉末,隨著哈密頓四元數理論的建立,非交換代數的研究已經開始. 在十九世紀下半葉,隨著M.S.李的工作,非結合代數出現了. 到二十世紀初,由於放棄實數體或複數體作為運算元域的限制,代數得到了重大擴展。
與外代數,對稱代數,張量代數,克利福德代數等一起,代數結構在多重線性代數中也建立了起來。
環
環是抽象代數的一個基本概念。如果在一個非空集合S中,定義了兩種代數運算:“加法”與“乘法”,S關於加法構成交換群,關於乘法滿足結合律及對於加法的分配律,就稱集合S關於所定義的運算構成一個環。如果乘法還滿足交換律,就稱為交換環。以數為元素的環,稱為數環。例如,整數的全體或有理數的全體都構成環,但正整數的全體就不是環,因為對加法,它不存在元素零及逆元素(負整數)。
對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類。如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則稱F為Ω上的環。例如,若F是由實直線R上任意有限個左開右閉的有限區間的並集:
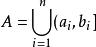 可除代數
可除代數的全體構成的集類,則F是R上的一個環.環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環。要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。
除環
亦稱體或斜域。接近於域的一類條件很強的環。設R是一個有單位元的環.若R中至少含有一個非零元,且每個非零元都是可逆元,則稱R為除環。交換的除環是域。
除環(division ring),又譯反稱域或體(skew field)、體,是如下定義的一個環:
至少有一個非零元素,這些非零元素稱為單位(Unit)。
非零元素都存在逆元素(左逆元素與右逆元素)。
它和域(field)的區別在於除環不必要符合交換律。所有域都是除環。不符合交換律的除環(斜體),例子有四元數體。
可除代數重要定理
弗羅貝尼烏斯定理是可除代數的一個重要定理。該定理是特徵對合分布的一個著名定理。該定理斷言:C流形上的C分布D為對合的充分必要條件為它是完全可積的。在任一坐標圖(U,φ,x)上,l維分布D等價於普法夫方程組φ=0,其中t=l+1,l+2,…,n(=dim M),D為對合等價於外微分方程組:
dφ=0 mod(φ,φ,…,φ);
而D為完全可積則等價於子流形:
{x∈U|x=const, l+1≤t≤n}
適合普法夫方程組φ=0。這樣的普法夫方程組也稱為是完全可積的。因此,弗羅貝尼烏斯定理也可以敘述為:普法夫方程組ω=0 (1≤α≤m)完全可積的充分必要條件是dω=0 mod(ω,ω,…,ω)。
