簡介
反卷積是信號處理中一類基本問題,廣泛套用於信道均衡、圖像恢復、語音識別、地震學、無損探傷等領域,也可套用於未知輸入估計和故障辨識問題。
一般來說，反卷積的目的是找到一個形式的卷積方程的解：
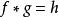反卷積
反卷積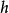
反卷積 反卷積 反卷積 反卷積 反卷積通常，是一些記錄的信號，f是我們希望恢復的一些信號，但是在我們記錄它之前已經與其他一些信號卷積。 函式可以表示儀器的傳遞函式或套用於物理系統的驅動力。 如果我們知道或者至少知道的形式，那么我們可以執行確定性反卷積。 但是，如果我們不知道，那么我們需要估計它。 這通常是使用統計估計方法完成的。
在物理測量中，通常更接近：
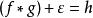反卷積
反卷積 反卷積在這種情況下是進入我們記錄的信號的噪音。 如果我們假設當我們嘗試對進行統計估計時噪聲信號或圖像是無噪聲的，那么我們的估計將是不正確的。 反過來，我們對f的估計也是不正確的。 信噪比越低，我們對解卷積信號的估計就越差。 這就是信號逆濾波通常不是一個好的解決方案的原因。 但是，如果我們至少有一些關於數據中噪聲類型的知識（例如，白噪聲），我們可能能夠通過諸如維納解卷積等技術來改進對f的估計。
反卷積反卷積通常是通過計算記錄信號h的傅立葉變換和傳遞函式，在頻域中套用解卷積來實現的，在沒有噪聲的情況下這僅僅是：
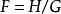反卷積
反卷積
反卷積
反卷積
反卷積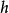 反卷積 反卷積，和分別是，和的傅立葉變換。 最後進行逆傅立葉變換F以找到估計的解卷積信號f。
反卷積和時間序列分析的基礎很大程度上由麻省理工學院的諾伯特·維納在他的書“外推，插值和平穩時間序列的平滑”（1949）中確定的。這本書是根據維納在第二次世界大戰期間所做的工作製作的，但那時是保密的。 套用這些理論的一些早期嘗試是在天氣預報和經濟學領域。
反卷積的套用
地震學
反卷積
反卷積
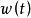反卷積反卷積概念在反射地震學中早有套用。 1950年，恩德斯羅賓遜是麻省理工學院的研究生。 他與麻省理工學院的其他人一起工作，如諾伯特維納，諾曼萊文森和經濟學家保羅薩繆爾森，以開發反射地震記錄的“卷積模型”。 該模型假設記錄的地震圖是來自點源的地球反射率函式和地震子波的卷積，其中t表示記錄時間。 因此，我們的卷積方程是
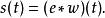反卷積
反卷積地震學家對非常感興趣，其中包含有關地球結構的信息。 通過卷積定理，該方程可以被傅立葉變換為
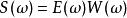反卷積在頻域, 通過假設反射率為白色，我們可以假設反射率的功率譜是恆定的，並且地震圖的功率譜是小波的頻譜乘以該常數。 從而，
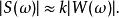反卷積如果我們假設小波是最小相位，我們可以通過計算我們剛發現的功率譜的最小相位等效來恢復它。 反射率可以通過設計和套用維納濾波器來恢復，該維納濾波器將估計的小波形成為狄拉克德爾塔函式（即尖峰）。 結果可能被看作是一系列縮放，移位的delta函式（儘管這在數學上並不嚴格）：
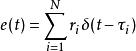反卷積其中N是反射事件的數量，τiτi是每個事件的反射時間，r i是反射係數。
實際上，由於我們正在處理噪聲，有限頻寬，有限長度，離散採樣的數據集，因此上述過程僅產生解卷積數據所需的濾波器的近似值。 然而，通過將問題表述為Toeplitz矩陣的解和使用Levinson遞歸，我們可以相對快速地估計具有最小均方誤差的濾波器。 我們也可以直接在頻域進行解卷積，並得到相似的結果。 該技術與線性預測密切相關。
光學等影像
在光學和成像領域，術語“反卷積”專指用於反轉在光學顯微鏡，電子顯微鏡，望遠鏡或其他成像儀器中發生的光學畸變的過程，從而創建更清晰的圖像。 它通常通過軟體算法在數字領域完成，作為一套顯微鏡圖像處理技術的一部分。 反卷積對於銳化在捕捉過程中受到快速運動或抖動影響的圖像也是實用的。 早期的哈勃太空望遠鏡圖像被一個有缺陷的鏡子扭曲，並可能被解卷積銳化。
通常的方法是假定通過儀器的光學路徑是光學理想的，與點擴散函式（PSF）卷積在一起，即數學函式，該數學函式描述光路理論點源（或 其他波）通過儀器。通常，這樣的點源對最終圖像貢獻了小範圍的模糊性。 如果可以確定這個函式，那么計算它的反函式或互補函式，並將獲取的圖像與其進行卷積。 結果是原始的，未失真的圖像。
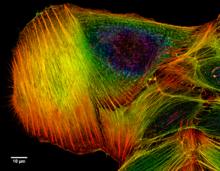圖一在實踐中，找到真正的PSF是不可能的，並且通常使用它的近似值，理論上計算或基於使用已知探針的一些實驗估計。 真實光學器件在不同的焦點和空間位置也可能具有不同的PSF，並且PSF可能是非線性的。 PSF逼近的準確性將決定最終結果。 以更加計算密集的價格，可以採用不同的算法來提供更好的結果。 由於原始卷積丟棄數據，一些算法使用附近焦點處獲取的附加數據來彌補一些丟失的信息。 疊代算法中的正則化（如期望最大化算法）可用於避免不切實際的解決方案。
當PSF未知時，可以通過系統地嘗試不同的可能的PSF並評估圖像是否改善來推斷PSF。 這個過程被稱為盲解卷積。盲反卷積在天文學中是一種成熟的圖像恢復技術，拍攝對象的點本質暴露了PSF，從而使其更加可行。 它還用於螢光顯微鏡中的圖像恢復，以及螢光光譜成像，用於多種未知螢光團的光譜分離。 為此目的最常用的疊代算法是Richardson-Lucy反卷積算法; 維納反卷積（和近似）是最常見的非疊代算法。
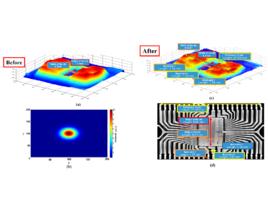
對於一些特定的成像系統，如雷射脈衝太赫茲系統，PSF可以用數學方法進行建模。 結果，如圖所示，模擬PSF和太赫茲圖像的反卷積可以給出太赫茲圖像的更高解析度表示。
射電天文學
在無線電干涉測量中進行圖像合成時，一種特定類型的射電天文學，一步包括將產生的圖像與“髒波束”解卷積，這是點擴散函式的不同名稱。 一種常用的方法是CLEAN算法。
傅立葉變換方面
反卷積映射到傅立葉共域中的劃分。 這使得反卷積可以很容易地套用於經受傅立葉變換的實驗數據。 一個例子是NMR譜，其中數據記錄在時域中，但是在頻域中進行分析。 通過指數函式對時域數據進行劃分具有減少頻域中洛倫茲線寬度的效果。
