概述
通常按照問題的實際情況選取適當的參考體。例如,當火箭從地球表面起飛時,宜用地球做參考體;當太空飛行器成為繞太陽運動的人造行星時,宜用太陽做參考體。由此可見,一切力學現象只能相對於所選定的參考系進行觀察、描述和研究。在同一參考繫上可有不同的參考坐標系,它們對同一個物體的位置坐標的值雖然不同,但有確定的幾何關係聯繫著。為了能對物體運動作定量描述,常直接引用參考坐標系。按牛頓的觀點,絕對運動是相對於絕對靜止參考系而言的。這就是說,自然界中存在一絕對靜止的空間,即絕對空間。根據近代的觀點,絕對空間並無客觀意義。19世紀的物理學家為了解釋J.麥克斯韋的電磁理論與牛頓力學中相對性原理的矛盾,曾假設空間充滿一種沒有質量且不流動的彈性介質“以太”(ether),電磁波被看成“以太”的振動。相對於“以太”靜止的參考系就代表絕對靜止的參考系。在此參考系中的電磁現象具有特殊性質,從而導致慣性坐標系對於描述電磁現象是不均等的論點。1887年A.邁克耳孫和E.莫雷發表的著名的實驗結果,表明“以太”效應是不能檢測到的。此後其他一些實驗也表明不能找到靜止參考系。因此,愛因斯坦指出,絕對靜止是根本沒有的。
愛因斯坦在1905年發表的著名論文《論動體的電動力學》中提出了狹義相對論兩條基本假設,即相對性原理和光速不變性。這兩條假設是狹義相對論的基礎,許多牛頓力學所不能解釋的現象,可用狹義相對論精確地描述。愛因斯坦的相對性原理指出:包括力學、電動力學、光學等在內的物理學各定律,在所有慣性參考系中都是相同的。即慣性坐標系對描述物理現象是平等的,沒有特殊的絕對靜止的參考系,絕對空間是無意義的。
慣性參考系
對慣性定律成立的參考系,簡稱慣性系。經典力學的相對性原理指出,一切力學規律在相互作勻速運動而無轉動的參考系中都是相同的。在一個作勻速直線運動的密封座艙中的觀察者,無法通過內部的力學實驗來判斷座艙相對於恆星是靜止的還是在作勻速運動的,只有朝窗外看才能知道,但仍然無法判斷究竟是座艙還是恆星在運動。另一方面,參考系在力學上的這種等效,並非對任意運動的參考系都成立。在顛簸運行的火車裡和在作勻速運動的火車裡,力學運動並不服從同樣的定律。在精確地相對於地球運動時,運動方程必須考慮地球的轉動。一個參考系,如果自由質點在其中作非加速運動,就稱為慣性參考系或伽利略參考系,所有相互作非加速運動而無轉動的參考系都是慣性參考系。判斷一個特定參考系是否慣性系,取決於能以多大的精確度去測出這個參考系的微小加速度效應。在地面上的一般工程動力學中,由於地球的自轉角速度較小,地面上一點的向心加速度很小,可取與地球固連的坐標系作為慣性系。在一些必須把地球自轉計算在內的問題中,如研究陀螺儀表的漂移時,可採用地球中心坐標系作為近似的慣性系,其原點與地球中心重合,軸指向所認定的恆星。天文學中則採用黃道坐標系或銀道坐標系作為慣性系。地球表面赤道上一點的向心加速度為3.4cm/s,地球繞太陽公轉的向心加速度為0.6cm/s,太陽繞銀河系中心轉動的向心加速度約為3×10cm/s。從以上數據可看出所選取的慣性系的近似程度。
非慣性參考系
對慣性參考系作加速運動或轉動的參考系,簡稱非慣性系。對慣性系以不變的加速度a在運動的非慣性系,稱為加速運動參考系。在此參考系中靜止的物體必有力F=ma作用著。在引力場中,物體都受引力作用,因此對引力場中慣性系靜止的物體也受引力作用。若另有一非慣性系,它對慣性系的加速度和這引力產生的加速度相同,則在此非慣性系中的觀察者並不覺得有引力場,也不知自己有加速運動,這就是愛因斯坦的“升降機”,說明引力場和非慣性系是等效的。對慣性參考系轉動的參考系稱為轉動參考系。假定慣性系靜止,則與轉動參考系固連的剛體運動,就是轉動參考系對慣性系的運動。對轉動參考系以速度vr和加速度ar運動的質點,按照點的複合運動公式,得質點對慣性參考系中的坐標系的加速度:
a=a0+ar+2ω×vr+ε×r′+ω×(ω×r),
式中a0為轉動坐標原點的加速度;ar為質點相對於轉動參考系的加速度;ω和ε分別為轉動坐標系的角速度和角加速度;r和r′分別為質點對慣性坐標系的原點和轉動坐標系的原點的矢徑。質點的相對運動方程可以表示為:
mar=F+(-2mω×vr)+[-mω×(ω×r)] +(-ma0-mε×r′) (1)
上式右邊第二項是科里奧利慣性力(簡稱科氏力);後三項是牽連慣性力,其中-mω×(ω×r)是離心慣性力。科氏慣性力對相對運動不作功,可從科氏慣性力恆和路徑垂直看出。因此科氏慣性力不能用勢函式表示。若轉動坐標原點不動(a0=0),並以等角速度ω(ε=0)繞Z軸轉動,選Z′軸與Z軸重合,則式(1)成為:
mar=F+(-2mω×vr)+[-mω×(ω×r)](2)
在研究地球自轉對地面鄰近物體運動的影響時,常用赤道坐標系。因地球繞太陽公轉角速度是地球自轉角速度的1/365,故可略去。選定Oxyz為慣性坐標系,Z軸與地球自轉軸重合,Oxy平面重合於赤道,X軸指向遙遠的恆星。地球自轉一周需23小時56分4.1秒,即86164.1太陽秒,故ω=2π/86164.1s=7.2921×10s。研究太陽系各行星的運動要用黃道坐標系。為研究天體現象與觀察者位置的相互關係還可引入地平坐標系,即Z軸指向觀察者的天頂。Oxy即地平面,X軸可選指向南,Y軸向東。研究星系力學和星繫結構則須採用以銀河系平均平面為基本面的銀道坐標系。
參考系和相對性
經典力學相對性原理是:一切力學定律在一切慣性系中都是相同的。各慣性坐標系是用伽利略變換聯繫起來的。設有兩個參考系S(Oxyz)及S'(O'x'y'z'),坐標軸相互平行且軸x與軸x'重合,S'相對S沿x軸以u做等速直線運動,且S系與S'系中各處有結構完全相同的時鐘,記錄的時刻為t與t',並以兩坐標原點O及O'重合時刻為計時起點,則可得某質點m的運動在兩參考系中的時空變換關係:x'=x-ut y'=y z'=z t'=t
上式即為伽利略(坐標)變換。如果將各式對時間求導,則得速度變換式:
vx'=vx-u vy'=vy vz'=vz
因此,如果S是慣性系,即不受外力作用的物體在其中做等速直線運動,則根據上式,它在S'中也一定做等速直線運動,所以S'也是慣性系。如果將各式再一次對時間求導,則得加速度變換關係式:
ax'=ax ay'=ay az'=az
亦即a'=a。因此如果S是慣性系,即在其中F=ma成立,則在S'中也有F=ma',所以S'也是慣性系。伽利略變換表明,加速度是不變數。此外,在經典力學中的力F和質量m都是不變數。因此,牛頓定律對伽利略變換是不變的,即一切力學定律在以伽利略變換聯繫起來的兩個慣性系中都是相同的,這就是經典力學的相對性原理。
狹義相對性原理可表述為:一切物理定律在以洛倫茲變換聯繫起來的兩個慣性系中具有不變性。這個原理比伽利略不變性更為普遍,它把力學定律、電磁和光的定律以及原子物理的定律等都包括在內。洛倫茲變換式為:
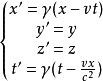
式中γ=[1-(v/c)],c為真空中的光速,v為慣性系S'(O'x'y'z')相對於S(Oxyz)的速度值,其方向沿X軸,大小與光速可以比擬。這裡的時間t′既是坐標x也是時間t的函式。因此,時間不能認為是對一切觀察者都相等的絕對量,而是依賴於觀察者位置和速度的相對量。這裡的空間、時間都是相對的,時間與空間緊密相關。洛倫茲變換中的這種時空關係導致了“四維時空”的概念,其中x、y、z和t起著類似而不盡相同的作用。至此歷史上麥克斯韋電磁場方程和伽利略不變性之間的矛盾便被狹義相對論圓滿地解決了。
廣義相對性原理認為所有參考系,不論是慣性系還是非慣性系,都同樣適合表達自然界定律,但需要用協變張量計算,把自然界定律表示成一個在任意坐標變換下保持不變的數學形式,這條原理又稱廣義協變性原理。據此,物理定律對洛倫茲變換也是協變的。在廣義相對論中,為了包括萬有引力,時間流逝的速度不僅與物體的運動速度有關,而且還與物體所受到的引力場有關。在引力場較大的地方,如在太陽附近,時間的流逝速度將變慢。
參考系和等效原理
慣性質量與引力質量的相等稱為等效原理。這個原理導致一個結論:一個存在著引力場的慣性系和另一個作加速運動的非慣性系是等效的,即內部的物理實驗不能區分這兩種參考系,這就是愛因斯坦等效原理。以愛因斯坦“升降機”為例,若升降機在1g的均勻引力場中靜止;另外,又在自由空間中以9.81m/s的加速度向上作勻加速運動,由於慣性質量和引力質量相等,在上述兩種情況中所作的同樣的內部物理實驗結果相同。裡面的觀察者既可認為升降機靜止,且機廂記憶體在引力場;又可認為機廂內不存在引力場,只是升降機以9.81m/s的加速度向上運動。慣性質量和引力質量的等效導致另一種情況。若一物體在均勻引力場中自由下落,其中的質點,由於慣性質量和引力質量相等,其慣性力和引力平衡。因此,同均勻引力場中自由降落的物體相固結的非鏇轉參考系和自由空間的慣性系是等效的。在環繞地球飛行的宇宙飛船中,“失重”現象就是由於引力和離心慣性力平衡所引起的。
慣性質量和引力質量的相等常稱為弱等效原理,愛因斯坦的等效原理則稱為強等效原理。等效原理是廣義相對論的基礎。
