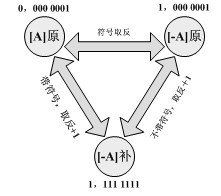
原碼的優點
簡單直觀;例如,我們用8位二進制表示一個數,+11的原碼為00001011,-11的原碼就是10001011
原碼的缺點
 原碼
原碼原碼不能直接參加運算,可能會出錯。例如數學上,1+(-1)=0,而在二進制中00000001+10000001=10000010,換算成十進制為-2。顯然出錯了。
所以原碼的符號位不能直接參與運算,必須和其他位分開,這就增加了硬體的開銷和複雜性
具體定義還分小數和整數:
①小數原碼的定義
[X] =
X( 0≤X <1 )
1- X (-1 < X ≤ 0)
例如: X=+0.1011 , [X]原= 0.1011
X=-0.1011 [X]原= 1.1011
②整數原碼的定義
[X]原 =
X (0≤X <2(n-1))
2(n-1)-X (- 2(n-1) < X ≤ 0)
x為正整數時,[X]原=x;
x為負整數時,[X]原=2的n次方-x;
x為負小數時,[X]原=1-x;
計算機中所有的數均用0,1編碼表示,數字的正負號也不例外,如果一個機器數字長是n位的話,約定最左邊一位用作符號位,其餘n-1位用於表示數值。
在符號位上用"0"表示正數;用"1"表示負數。數值位表示真值的絕對值。凡不足n-1位的,小數在最低位右邊加零;整數則在最高位左邊加零以補足n-1位。這種計算機的編碼形式叫做原碼。
記作X=[X]原。例如在字長n=8的機器內:
小數: [+0.1011]原=0.1011000
[-0.1011]原=1.1011000
整數: [+1011]原=00001011
[-1011]原=10001011
代碼中的小數點”.”是在書寫時為了清晰起見加上去的,在機器中並不出現。
編碼方式
 原碼
原碼 原碼
原碼原碼是有符號數的最簡單的編碼方式,便於輸入輸出,但作為代碼加減運算時較為複雜。一個字長為n的機器數能表示不同的數字的個數是固定的2^n個,n=8時2^n=256;用來表示有符號數,數的範圍就是-(2^(n-1)-1)~+2^(n-1)-1,n=8是這個範圍就是-127~+127。但是在不需要考慮數的正負時,就不需要用一位來表示符號位,n位機器數全部用來表示是數值,這時表示數的範圍就是0~2^n-1,n=8時這個範圍就是0~255.沒有符號位的數,稱為無符號數。(編輯器無法表示上標下標,可查閱圖片)