定理內容
博特周期性定理描述了酉群的同倫群和正交群同倫群的周期性。 簡單的講：
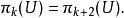博特周期性定理
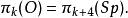博特周期性定理
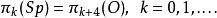博特周期性定理注意第2和第3個等式蘊涵了正交群的同倫群具有周期8。拉烏爾·博特開始是用莫爾斯理論證明的，後來又出現了K理論的證明。
莫爾斯理論
在微分拓撲中， 莫爾斯理論的技術給出了一個非常直接的分析一個流形的拓撲的方法，它是通過研究該流形上的可微函式達成。根據莫爾斯的基本見解，一個流形上的一個可微函式在 典型的情況下，很直接的反映了該流形的拓撲。莫爾斯理論允許人們在流形上找到CW結構和柄分解，並得到關於它們的同調群的信息。在莫爾斯之前，凱萊和麥克斯韋在製圖學的情況下發展了莫爾斯理論中的一些思想。莫爾斯最初將他的理論用於測地線（路徑的能量函式的臨界點）。
K-理論
在數學中， K-理論（K-theory）是多個領域使用的一個工具。在代數拓撲中，它是一種異常上同調，稱為拓撲K-理論；在代數與代數幾何中，稱之為代數K-理論；在運算元代數中也有諸多套用。它導致了一類 K-函子構造，K-函子包含了有用、卻難以計算的信息。
在物理學中，K-理論特別是扭曲K-理論出現在第二型弦理論，其中猜測它們可分類D-膜、拉蒙-拉蒙場以及廣義複流形上某些旋量。具體細節參見K-理論 (物理)。
另見
•上同調論列表
•K-理論 (物理)
•L-理論
•博特周期性
•拓撲K-理論
•Todd class
