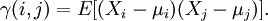簡介
在統計學中，特定時間序列或者連續信號 X的 自協方差是信號與其經過時間平移的信號之間的協方差。如果序列的每個狀態都有一個平均數E[ X]=μ，那么自協方差為
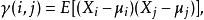自協方差其中E是期望值運算符。如果 X是二階平穩過程，那么有更加常見的定義：
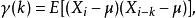自協方差其中k是信號移動的量值，通常稱為延時。如果用方差σ進行歸一化處理，那么自協方差就變成了自相關係數R(k)，即
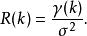自協方差需要注意的是，在有些學科中自協方差術語等同於自相關。
可以認為自協方差是某個信號與其自身經過一定時間平移之後的相似性，自協方差σ就表示了在那個時延的相關性。經過方差的歸一化處理將其範圍轉化為[−1,1]。
協方差
協方差（Covariance）在機率論和統計學中用於衡量兩個變數的總體誤差。而方差是協方差的一種特殊情況，即當兩個變數是相同的情況。
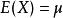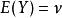自協方差
自協方差期望值分別為與的兩個實數隨機變數 X與 Y之間的 協方差定義為：
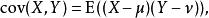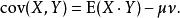自協方差
自協方差協方差表示的是兩個變數的總體的誤差，這與只表示一個變數誤差的 方差不同。 如果兩個變數的變化趨勢一致，也就是說如果其中一個大於自身的期望值，另外一個也大於自身的期望值，那么兩個變數之間的協方差就是正值。 如果兩個變數的變化趨勢相反，即其中一個大於自身的期望值，另外一個卻小於自身的期望值，那么兩個變數之間的協方差就是負值。
如果X與Y是統計獨立的，那么二者之間的協方差就是0，這是因為
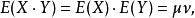自協方差但是反過來並不成立，即如果X與Y的協方差為0，二者並不一定是統計獨立的。取決於協方差的相關性η
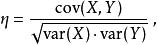自協方差更準確地說是線性相關性，是一個衡量線性獨立的無量綱數，其取值在[－1,+1]之間。相關性η = 1時稱為“完全線性相關”（相關性η = －1時稱為“完全線性負相關”），此時將Y對X作Y-X散點圖，將得到一組精確排列在直線上的點；相關性數值介於－1到1之間時，其絕對值越接近1表明線性相關性越好，作散點圖得到的點的排布越接近一條直線。
相關性為0（因而協方差也為0）的兩個隨機變數又被稱為是不相關的，或者更準確地說叫作“線性無關”、“線性不相關”，這僅僅表明X與Y兩隨機變數之間沒有線性相關性，並非表示它們之間一定沒有任何內在的（非線性）函式關係，和前面所說的“X、Y二者並不一定是統計獨立的”說法一致。
平穩過程
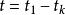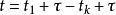自協方差
自協方差在數學中， 平穩過程（英語：Stationary process），又稱 嚴格平穩過程（英語：Strict(ly) stationary process）或 強平穩過程（英語：Strong(ly) stationary process）是一種特殊的隨機過程，在其中任取一段期間或空間（）里的聯合機率分布，與將這段期間任意 平移後的新期間（）之 聯合機率分布相等。這樣，數學期望和方差這些參數也不隨時間或位置變化。
例如，白噪聲（AWGN）就是平穩過程，鐃鈸的敲擊聲是非平穩的。儘管鐃鈸的敲擊聲基本上是白噪聲，但是這個噪聲隨著時間變化：在敲擊前是安靜的，在敲擊後聲音逐漸減弱。
在時間串列分析中穩態作為一個工具使用，在這裡原始數據經常轉換為平穩態，例如經濟學數據經常隨著季節或者價格水平變化。如果這些過程是平穩過程與一個或者多個呈現一定趨勢的過程的線性組合，那么這些過程就可以表述為趨勢平穩。將這些數據進行轉換保留平穩數據用於分析的過程稱為 解趨勢（de-trending）。
採樣空間也是離散的離散時間平穩過程稱為Bernoulli scheme，離散採樣空間中每個隨機變數可能取得N'個可能值中的任意一個。當N= 2 的時候，這個過程叫做伯努利過程。
自相關函式
自相關（英語： Autocorrelation），也叫 序列相關，是一個信號於其自身在不同時間點的互相關。非正式地來說，它就是兩次觀察之間的相似度對它們之間的時間差的函式。它是找出重複模式（如被噪聲掩蓋的周期信號），或識別隱含在信號諧波頻率中消失的基頻的數學工具。它常用於信號處理中，用來分析函式或一系列值，如時域信號。
