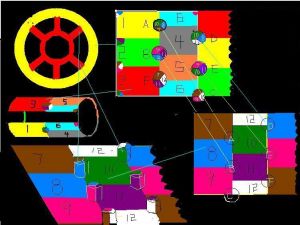
一摘要
有7個洞的曲面有12個區域兩兩相連,儘管林格和楊斯在1974年已經證明,但是一直沒有人構造出來。 王曉明王蕊珂構造,人民郵電出版社258頁。
二,十二色定理七)虧格7時有12個區域兩兩相連
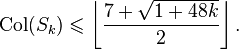 公式
公式N7==12,參見圖8,右上圖是外環平面圖,有6個區域兩兩相連,先上下對摺,再左右對摺,左右對摺時一段輕輕扭轉,使得區域1對著區域5,區域2對著區域6,區域3對著區域4。右下圖和左下圖是內環,上下對摺再左右對摺形成一個輪胎形狀,左右對摺時一端輕輕扭轉,使得區域7對摺區域11,區域8對著區域12,區域9對摺區域10。外部有6根柱子與外環相連,形成一個有7個洞的12個區域兩兩相連,王曉明虛構。 二, 證明部分在證明四色定理過程中,
Heawood的文章不僅僅指出,而且也給出了五色定理的一個證明,然而他沒有停留於此,Heawood繼續考慮其它一些想法,Heawood文章的主要後續成果是征對於可嵌入到球面的圖的最大色數問題。Heawood把注意力轉移到其它曲面上圖的色數確定問題上。三,虧格6時按照公式應該有12個區域兩兩相連。至今沒有人能夠畫出。對於非負整數k,設
χ(Sκ)=max{χ(G)}.
其中,max取遍嵌入到Sx的所有圖G,自Kempe的1879年的文章之後,大家都相信χ(Sò)=4,而在Heawood的1890年的文章之後,僅僅知道χ(Sò)=4,或者χ(Sò)=5.
1976年當Appel和Haken宣布其成果之後,確定了χ(Sò)=4(四色定理)。
在Heawood的1890年的文章中,他試圖獲得關於χ(Sκ)的一個公式,在其中k為正整數,事實上,他認為他已經做到了,然而,他所做的僅僅是獲得了χ(Sκ)的一個上界。
定理;對於每一個正整數k,
χ(Sκ)≤[(7+√1+48K))/2]
證明:(直接證法)設G為看嵌入到Sκ的一個圖,並且設
h=[(7+√1+48K)/2],
由h的定義可以證明:
6+12(k-1)/h=h-1
下面證明χ(G)≤h
在G的所有誘導子圖中,設H具有最大的最小度,根據定理:對每個圖G,
X(G)<1+max{S(H)}
其中,max取遍G的所有誘導子圖H。
可以得到X(G)≤1+δ(H),假設H的階為n,邊數為m,若n≤h,則δ(H)≤n-1,X(G)≤n≤h,因此我們可以假設n>h.
由於G可以嵌入到Sk,所以,H也能夠嵌入到Sk,因此由推論可知
K>γ(H)≥m/6-n/2+1,
易見,m≤3n+6(k-1),因此nδ(H)≤Σdegu=2m≤6n+12(k-1)所以,
δ(H)≤6+12(k-1)/n≤6+12(k-1)/h=h-1。從而,X(G)≤1+δ(H)=h=[(7+√1+48k)/2]。
,結論成立。
證明這個公式對於所有整數k成立又花費了78年。數學家GerhardRingel和TedYoung對這個公式的證明發揮了最主要的作用。