概念
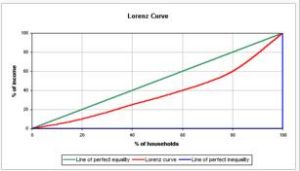
在經濟學里，勞倫茲曲線是在過往財富分配數據上建立的累積分布函式所對應的曲線，它通過變數y%的值來反映各項分配的比例。它經常被用來描述收入的分配情況，即以x%代表一部分(收入相似)家庭占整個社會家庭的比例，以y%代表該部分家庭的收入占整個社會收入的比例。該曲線也可用來描述社會資本的分配情況。在這些套用當中，經濟學家經常把它用來衡量社會(主要指社會收入)是否公平。機率密度函式（f（x））或累積分布函式（F（x））：
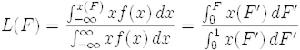勞倫茨曲線這曲線在發展經濟學上，除了用於常見的基尼係數表示收入分布，還有土地分布，教育度的程度的分布等。
基於勞倫茨曲線之上的基尼係數，被用來定量測定社會居民收入分配的差異程度，一般只有高於0.4，才會被認為社會收入分配不公。
舉例
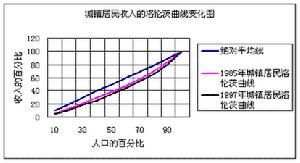圖1：城鎮居民收入的洛倫茨曲線變化圖勞倫茨曲線的弧度越小，基尼係數也越小。基尼指數，又譯基尼係數及堅尼係數，是20世紀初義大利經濟學家基尼，根據勞倫茨曲線找出了判斷分配平等程度的指標。
設實際收入分配曲線和收入分配絕對平等曲線之間的面積為A，實際收入分配曲線右下方的面積為B。並以A除以A+B的商表示不平等程度。這個數值被稱為基尼係數或稱勞倫茨係數。如果A為零，基尼係數為零，表示收入分配完全平等；如果B為零則係數為1，收入分配絕對不平等。該係數可在零和1之間取任何值。收入分配越是趨向平等，勞倫茨曲線的弧度越小，基尼係數也越小，反之，收入分配越是趨向不平等，勞倫茨曲線的弧度越大，那么基尼係數也越大。如果個人所得稅能使收入均等化，那么，基尼係數即會變小。
世界各主要城市的基尼係數，聯合國有關組織規定：0.3-0.4表示相對合理；0.4-0.5表示收入差距較大；0.6以上表示收入差距懸殊。
根據以往的數據，描繪現階段（截至2000年）我國城鎮居民收入差距拉大的洛倫茨曲線。
圖1是筆者根據洛倫茨曲線原理作出的類似於洛倫茨曲線的圖形，採用十等分法，20%為一組的數據取其中值作為10%處的數據。這樣估算出的基尼係數略為0.25，考慮到十等分組中有三組的十等分組是按照絕對平均的中值來計算，人為將收入平均化了。另外，十等分組只是考慮到組間的差距，而沒有考慮到組內的差距，我國人口眾多，單純將居民收入劃分為十等分組不能夠科學地表現出真實的居民差距。所以，這裡得出的0.25的基尼係數可以說是1997年城鎮居民收入差距的底限，或者說是最低值。而僅僅以0.25來看，就比改革初期擴大了67個百分點。
