簡介
 雅可比符號
雅可比符號 雅可比符號
雅可比符號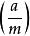 雅可比符號
雅可比符號 雅可比符號
雅可比符號 雅可比符號
雅可比符號 雅可比符號
雅可比符號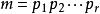 雅可比符號
雅可比符號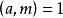 雅可比符號
雅可比符號雅可比符號(Jacobi symbol)是勒讓德符號的推廣,整數 對整數 的雅可比符號表示為 。設 是大於 的奇數,且 的素因數分解式為 (式中因數可以相同),如果 ,則雅可比符號定義為:
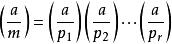 雅可比符號
雅可比符號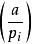 雅可比符號
雅可比符號 雅可比符號
雅可比符號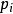 雅可比符號
雅可比符號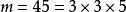 雅可比符號
雅可比符號其中, 是 對 的勒讓德符號。例如,取 ,則:
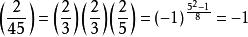 雅可比符號
雅可比符號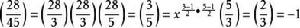 雅可比符號
雅可比符號註:雅可比符號是勒讓德符號的推廣,但是根據雅可比符號的值不能判斷同餘式是否有解。
定義補充說明
 雅可比符號
雅可比符號(1)當 是奇素數時,雅可比符號就是勒讓德符號。
 雅可比符號
雅可比符號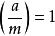 雅可比符號
雅可比符號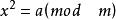 雅可比符號
雅可比符號(2)當 是奇素數且 時,方程 有解。當m不是奇素數時,這個結論不一定成立。
定理
定理1
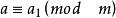 雅可比符號
雅可比符號(1)若 ,則
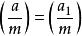 雅可比符號
雅可比符號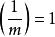 雅可比符號
雅可比符號(2)
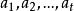 雅可比符號
雅可比符號(3)對於任意的整數 ,有
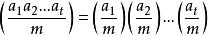 雅可比符號
雅可比符號(4)對於任意的整數a,b,(a,m)= 1,有
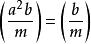 雅可比符號
雅可比符號定理2
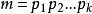 雅可比符號
雅可比符號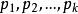 雅可比符號
雅可比符號設 是奇數,其中 是素數,則下面的結論成立:
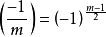 雅可比符號
雅可比符號(1)
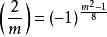 雅可比符號
雅可比符號(2)
定理3
設m,n是大於1的奇整數,則
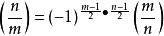 雅可比符號
雅可比符號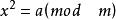 雅可比符號
雅可比符號利用以上定理,可以容易計算Jacobi符號,特別是Legendre符號的數值。但是,必須注意,在判斷方程 的可解性時,Legendre符號和Jacobi的作用是不一樣的。
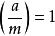 雅可比符號
雅可比符號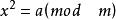 雅可比符號
雅可比符號對於一般的正奇數m來說,即使條件 成立,也並不能保證 一定有解。
舉例
例1
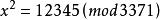 雅可比符號
雅可比符號已知3371是素數,判斷方程 是否有解。
解:利用Jacobi符號的性質,有
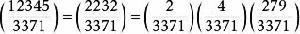 雅可比符號
雅可比符號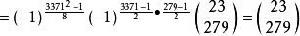 雅可比符號
雅可比符號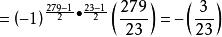 雅可比符號
雅可比符號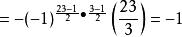 雅可比符號
雅可比符號因此,方程無解。
例2
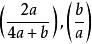 雅可比符號
雅可比符號設a與b是正奇數,求 的關係。
解:
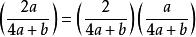 雅可比符號
雅可比符號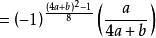 雅可比符號
雅可比符號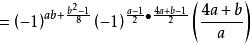 雅可比符號
雅可比符號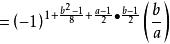 雅可比符號
雅可比符號