物理定義
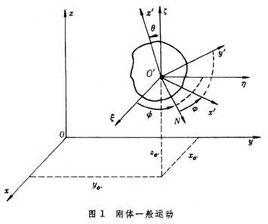
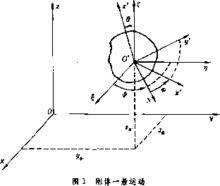剛體一般運動在剛體上取固連坐標系O'x'y'z'，並由基點O'作出平動坐標系O'ξηζ（圖1），則剛體對固定坐標系Oxyz的一般運動可被分解成隨基點O'的牽連平動和繞基點O的相對定點轉動。
基點O'的三個坐標xO'、yO'、zO'，以及O'x'y'z'對O'ξηζ的三個歐拉角ψ、θ、φ可確定一般運動剛體的位置。由此可見，剛體作一般運動時有六個自由度。
剛體的一般運動方程為：
xO'=f1(t)，yO'=f2(t)，zO'=f3(t)；
ψ=f4(t)，θ=f5(t)，φ=f6(t)。
特殊情況下，剛體有特定的運動方式：①如ψ、θ、φ都不變，表示剛體的平動；②如基點不動，則為剛體定點轉動；③如θ=φ=0，又zO'不變，則為剛體平面運動；④如θ=φ=0，又xO'、yO'都不變，則為剛體螺鏇運動（見剛體運動的合成）。
歐拉定理和夏萊定理
揭示剛體一般運動特性的有下述的歐拉定理和夏萊定理。
歐拉定理
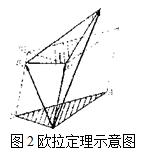
剛體一般運動剛體作一般運動時的任何位移都可分解為隨基點的平動位移和繞基點上某軸的
轉動位移，改變基點的選擇，只影響平動位移而不改變轉動位移的轉角。圖2中△ABC到△A1B1C1的位移可看成由兩步完成：先由ABC平移到A'1B'1C1，再繞通過C1的某軸轉過某角而到達A1B1C1，也可取A1或其他點作基點。
夏萊定理
剛體作一般運動時的任何位移都可化成螺鏇位移，由繞某軸的轉動和沿該軸的平動位移合成。這個軸稱為螺鏇軸。上面各點只有平動位移，此位移是剛體上各點的最小位移。
將夏萊定理套用於微小時間△t中的位移，則剛體的一般運動可歸結為在每瞬時沿著和繞著瞬時螺鏇軸的螺鏇運動。
隨著時間的推移，瞬時螺鏇軸在固定空間描出一個線生曲面，同時它在剛體內部也描出一個線生曲面。這兩個曲面相切於該瞬時的螺鏇軸。因此，剛體的一般運動可視為動曲面繞螺鏇軸的翻滾和沿該軸的滑動這兩種運動的合成。
當剛體作一般運動時，它的任一點的速度和加速度分別由相應的牽連分量和相對分量合成（見點的複合運動）。
